दो गोलीय तारों $A$ तथा $B$ के घनत्व क्रमश: $\rho_A$ तथा $\rho_B$ है। $A$ तथा $B$ की त्रिज्या समान है तथा इनके द्रव्यमान $M_A$ तथा $M_B$, $M_B=2 M_A$ से सम्बन्धित है। अन्योन्य क्रिया प्रक्रिया के कारण, तारें $A$ के कुछ द्रव्यमान की हानि होती है, ताकि इसकी त्रिज्या आधी हो जाती है, जबकि इसकी गोलाकार आकृति बनी रहती है तथा इसका घनत्व $\rho_A$ रहता है। $A$ द्वारा सम्पूर्ण द्रव्यमान हानि $B$ पर एक मोटे गोलाकार कोश के रूप में जमा हो जाती है जबकि कोश का घनत्व $\rho_A$ है। यदि $v_A$ तथा $v_B$ अन्योन्य क्रिया प्रक्रिया के बाद $A$ तथा $B$ से पलायन वेग है, तब अनुपात $\frac{v_B}{v_A}=\sqrt{\frac{10 n}{15^{1 / 3}}}$ है। $n$ का मान _________ है |

एक प्रयोगशाला तंत्र में एक अल्फा कण द्वारा नाभिकीय अभिक्रिया ${ }_7^{16} \mathrm{~N}+{ }_2^4 \mathrm{He} \rightarrow{ }_1^1 \mathrm{H}+{ }_8^{19} \mathrm{O}$ सम्पन्न करने के लिए आवश्यक न्यूनतम गतिज ऊर्जा $n$ ( $\mathrm{MeV}$ में) है। माना कि ${ }_7^{16} \mathrm{~N}$ प्रयोगशाला तंत्र में विराम में है। ${ }_7^{16} \mathrm{~N},{ }_2^4 \mathrm{He},{ }_1^1 \mathrm{H}$ तथा ${ }_8^{19} \mathrm{O}$ के द्रव्यमान क्रमशः $16.006 \mathrm{u}, 4.003 \mathrm{u}, 1.008 \mathrm{u}$ तथा $19.003 \mathrm{u}$ के रूप में लिये जा सकते है, जहाँ $1 \mathrm{u}=930 \mathrm{MeVc}^{-2}$ है। $n$ का मान _________ है।

निम्न परिपथ में $C_1=12 \mu \mathrm{F}, C_2=C_3=4 \mu \mathrm{F}$ तथा $C_4=C_5=2 \mu \mathrm{F}$ है। $C_3$ में संग्रहित आवेश _______ $\mu \mathrm{C}$ है।.

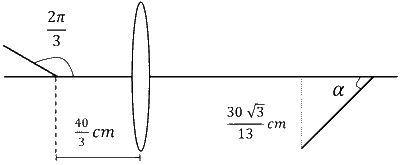
$2 \mathrm{~cm}$ लम्बाई की एक छड़ एक पतले उत्तल लेंस के मुख्य अक्ष के साथ $\frac{2 \pi}{3}$ रेडियन कोण निर्मित करती है। लेंस की फोकस दूरी $10 \mathrm{~cm}$ है तथा इसे चित्र में दर्शाए अनुसार वस्तु से $\frac{40}{3} \mathrm{~cm}$ की दूरी पर रखा जाता है। प्रतिबिम्ब की ऊँचाई $\frac{30 \sqrt{3}}{13} \mathrm{~cm}$ है तथा मुख्य अक्ष के सापेक्ष इसके द्वारा बनाया गया कोण $\alpha$ रेडियन है। $\alpha$ का मान $\frac{\pi}{n}$ रेडियन है, जहाँ $n$ __________ है।

समय $t=0$ पर, $1 \mathrm{~m}$ त्रिज्या की एक डिस्क किसी क्षैतिज तल पर बिना फिसले कोणीय त्वरण $\alpha=\frac{2}{3} \mathrm{rad} \mathrm{s}^{-2}$ से लुढ़कना प्रारम्भ करती है। एक छोटा पत्थर डिस्क से चिपक जाता है। $t=0$ पर, यह डिस्क के सम्पर्क बिन्दु तथा तल पर है। इसके पश्चात् समय $t=\sqrt{\pi} s$ पर, पत्थर स्वयं ही अलग हो जाता है तथा डिस्क से स्पर्शरेखीय रूप से गति करता है। तल से मापित पत्थर द्वारा प्राप्त की गई अधिकतम ऊँचाई ( $\mathrm{m}$ में) $\frac{1}{2}+\frac{x}{10}$ है। $x$ का मान __________ है। [ $g=10 \mathrm{~ms}^{-2}$ लीजिए]

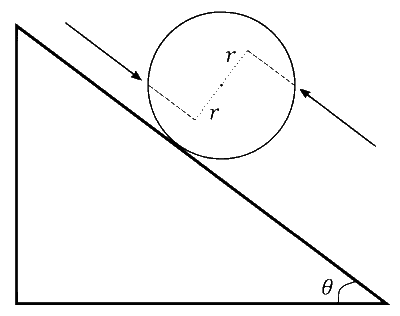
द्रव्यमान $1 \mathrm{~kg}$ तथा त्रिज्या $1 \mathrm{~m}$ का एक ठोस गोला क्षैतिज से आनति कोण $\theta=30^{\circ}$ के साथ एक रिथर आनत तल पर बिना फिसले लुढ़कता है। आनत के समान्तर समान परिमाण $1 \mathrm{~N}$ के दो बल चित्र में दर्शाए अनुसार गोले पर कार्य करते हैं, यह दोनों गोले के केन्द्र से दूरी $r=0.5 \mathrm{~m}$ पर है। तल पर नीचे की ओर गोले का त्वरण ________ $\mathrm{ms}^{-2}$ है। $\left(g=10 \mathrm{~ms}^{-2}\right.$ लीजिए)

एक तल पर रखे प्रेरकत्व $L=0.1 \mathrm{~H}$ तथा धारिता $C=10^{-3} \mathrm{~F}$ वाले एक $\mathrm{LC}$ परिपथ पर विचार कीजिए। परिपथ का क्षेत्रफल $1 \mathrm{~m}^2$ है। इसे $B_0$ सामर्र्य के एक नियत चुम्बकीय क्षेत्र में रखा जाता है, जो परिपथ के तल के लम्बवत् है। समय $t=0$ पर, चुम्बकीय क्षेत्र सामर्थ्य $B=B_0+\beta t$ के अनुसार रेखीय रूप से बढ़ना प्रारम्भ करता है तथा $\beta=0.04 \mathrm{~Ts}^{-1}$ है। परिपथ में धारा का अधिकतम परिमाण _________ $\mathrm{mA}$ है।

एक प्रक्षेप्य को क्षैतिज धरातल से $v$ चाल तथा प्रक्षेपण कोण $\theta$ से दागा जाता है। जब गुरूत्वीय त्वरण $g$ है, तब प्रक्षेप्य की परास $d$ है। यदि इसके प्रक्षेप पथ में उच्चतम बिन्दु पर, प्रक्षेप्य भिन्न-भिन्न क्षेत्रों में प्रवेश करता है, जहाँ प्रभावी गुरूत्वीय त्वरण $g^{\prime}=\frac{g}{0.81}$ है, तब नवीन परास $d^{\prime}=n d$ है। $n$ का मान ________ है।

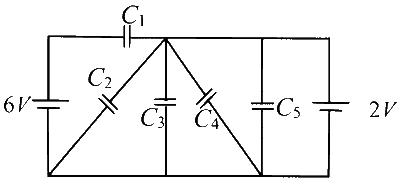
एक समान्तर प्लेट संधारित्र की प्लेटों के मध्य अंतराल को परावैद्युतांक $K>1$ वाले एक माध्यम से भरा जाता है। प्लेटों का क्षेत्रफल अत्यधिक है तथा इनके मध्य की दूरी $d$ है। संधारित्र को चित्र (a) में दर्शाए अनुसार वोल्टता $V$ की एक बैटरी से संयोजित किया जाता है। अब दोनों प्लेटों को चित्र (b) में दर्शाए अनुसार इनकी मूल स्थितियों से $\frac{d}{2}$ दूरी तक गति करायी जाती है।

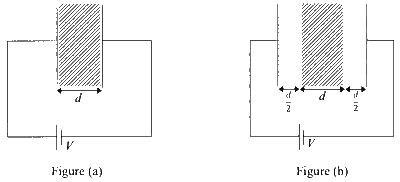
चित्र (a) में तथा चित्र (b) में प्रदर्शित अभिविन्यास से गुजरने वाली प्रक्रिया में, निम्नलिखित में कौनसा / कौनसे कथन सही है / हैं?

चित्र में $R_1$ से $R_8$ वाले $1 \Omega$ के आठ प्रतिरोधों तथा वोल्टता $\varepsilon_1=12 \mathrm{~V}$ तथा $\varepsilon_2=6 \mathrm{~V}$ वाली दो आदर्श बैटरियों का एक परिपथ दर्शाया गया है।

निम्नलिखित में से कौनसा / कौनसे कथन सही है / हैं?

एक आदर्श गैस, जिसका घनत्व $$\rho=0.2 \mathrm{~kg} \mathrm{~m}^{-3}$$ है, एक $$h$$ ऊँचाई की चिमनी के निचले सिरे से $$\alpha= 0.8 \mathrm{~kg} \mathrm{~s}^{-1}$$ की दर से प्रवेश करती है और ऊपर के सिरे से बाहर निकलती है, जैसा की चित्र में दर्शाया गया है। चिमनी का आनुप्रस्थ (cross-sectional) क्षेत्रफल निचले सिरे पर $$A_{1}=0.1 \mathrm{~m}^{2}$$ और उपरी सिरे पर $$A_{2}=0.4 \mathrm{~m}^{2}$$ है। गैस का दाब व ताप निचले सिरे पर क्रमशः $$600 \mathrm{~Pa}$$ और $$300 \mathrm{~K}$$ हैं जबकि ऊपरी सिरे पर गैस का ताप $$150 \mathrm{~K}$$ है। चिमनी उष्मा कुचालक (heat insulated) है ताकि गैस रुधोष्म प्रक्रम (adiabatic process) से प्रसारित (expand) होती है। $$g=10 \mathrm{~ms}^{-2}$$ तथा गैस विशिष्ट उष्माओ का अनुपात (ratio of specific heats) $$\gamma=2$$ मान लें वायुमंडलीय (atmospheric) दाब नगण्य है।

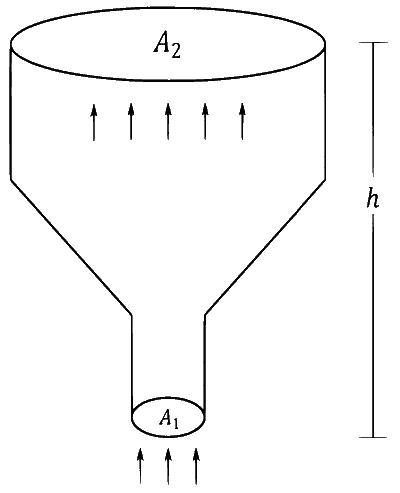
निम्न में से कौन सा(से) कथन सही है(हैं)|

तीन समतल दर्पण (plane mirror) एक समबाहू (equilateral) त्रिभुज बनाते हैं जिसकी प्रत्येक भुजा की लम्बाई $$L$$ है| त्रिभुज के एक कोने से $$l > 0$$ दूरी पर एक छोटा छिद्र है, जैसा कि चित्र में दर्शाया गया है। एक प्रकाश की किरण $$\theta$$ कोण पर छिद्र से अंदर जाती है तथा इसी छिद्र से बाहर आ सकती है। दर्पण संयोजन (configuration) की अनुप्रस्थ काट (cross section) तथा प्रकाश की किरण एक ही तल में हैं।

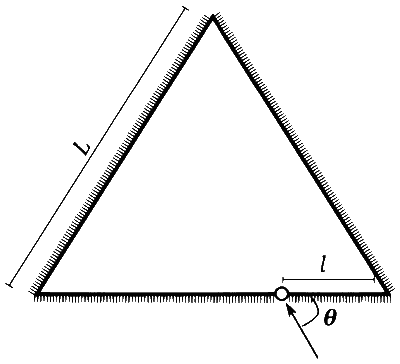
निम्न में से कौन सा(से) कथन सही है(हैं)?

छह आवेशों को एक नियमित षट्भुज (hexagon) जिसकी भुजा की लम्बाई $$a$$ है के परितः (around) रखा गया है, जैसा की चित्र में दर्शाया गया है। उनमें से पांच का आवेश $$q$$, तथा बचे हुए एक का आवेश $$x$$ है। प्रत्येक आवेश से षट्भुज की समीपतम भुजा पर डाला गया लम्बवत षटभुज के केंद्र $$\mathrm{O}$$ से गुजरता है तथा उस भुजा के द्वारा द्विभाजित (bisect) होता है।

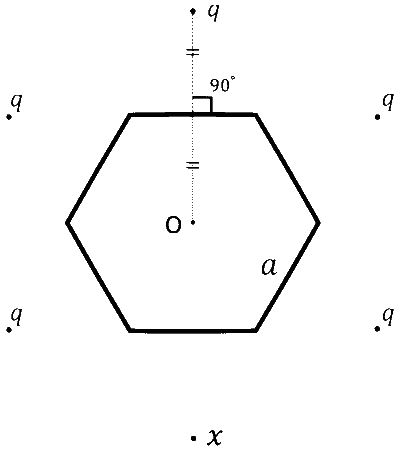
निम्न में से कौन सा(से) कथन SI मानक में सही है(हैं)?

एक नाभिक में नाभिकीय कणों (nucleons) की बंधक उर्जा (binding energy) युग्म कूलाम्ब प्रतिकर्षण (pairwise Coulomb repulsion) द्वारा प्रभावित हो सकती है। मान लें सभी नाभिकीय कण नाभिक के अंदर सामान रूप (uniformly) से वितरित है। दिया हुआ है कि प्रोटोन की बंधक उर्जा $$E_{b}^{p}$$ और न्यूट्रॉन की बंधक उर्जा $$E_{b}^{n}$$ है।

निम्न में से कौन सा(से) कथन सही है(हैं)?

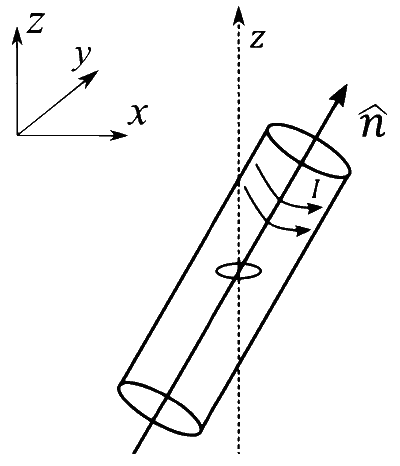
एक छोटा वृतीय छल्ला (circular loop) जिसका क्षेत्रफल $$A$$ तथा प्रतिरोध $$R$$ है, एक क्षैतिज (horizontal) $$x y$$-तल पर नियत किया गया है। छल्ले का केन्द्र हमेशा एक लम्बी परिनलिका (solenoid) के अक्ष $$\hat{n}$$ पर रहता है। इस परिनलिका में $$m$$ घुमाव प्रति मानक लम्बाई (turns per unit length) तथा धारा $$I$$ वामावर्त (anticlockwise) दिशा में हैं, जैसा कि चित्र में दर्शाया गया है। परिनलिका की वजह से चुम्बकीय क्षेत्र $$\hat{n}$$ दिशा में है। लिस्ट I में एकसमान कोणीय आवृति में $$\hat{n}$$ की समय पर आधारिता (dependences) दी गयी है। लिस्ट II में वृतीय छल्ले का बलआघूर्ण (torque) $$t=\frac{\pi}{6 \omega}$$ पर दिया गया है| $$\alpha=\frac{A^{2} \mu_{0}^{2} m^{2} I^{2} \omega}{2 R}$$ लें।

	सूची-I		सूची-II
(I)	$$\frac{1}{\sqrt{2}}(\sin \omega t \hat{\jmath}+\cos \omega t \hat{k})$$	(P)	0
(II)	$$\frac{1}{\sqrt{2}}(\sin \omega t \hat{\imath}+\cos \omega t \hat{\jmath})$$	(Q)	$$-\frac{\alpha}{4} \hat{\imath}$$
(III)	$$\frac{1}{\sqrt{2}}(\sin \omega t \hat{\imath}+\cos \omega t \hat{k})$$	(R)	$$\frac{3 \alpha}{4} \hat{\imath}$$
(IV)	$$\frac{1}{\sqrt{2}}(\cos \omega t \hat{\jmath}+\sin \omega t \hat{k})$$	(S)	$$\frac{\alpha}{4} \hat{\jmath}$$
		(T)	$$-\frac{3 \alpha}{4} \hat{\imath}$$

निम्न में से कौन सा एक विकल्प सही है?

लिस्ट $$\mathrm{I}$$ में चार तंत्र (system) वर्णित हैं, प्रत्येक में दो कण $$A$$ और $$B$$ की सापेक्ष गति (relative speed) का चित्रण किया गया है| लिस्ट $$\mathrm{II}$$ में उनकी सापेक्ष गति ($$\mathrm{m} \mathrm{s}^{-1}$$ में) का संभावित परिमाण समय $$t=\frac{\pi}{3} s$$ पर दिया गया है।

	सूची-I		सूची-II
(I)	$$A$$ तथा $$B$$ एक $$1 \mathrm{~m}$$ त्रिज्या के वृत पर एकसमान कोणीय गति $$\omega=1 \mathrm{rad} \mathrm{s}^{-1}$$ से घूमते हैं जहाँ $$A$$ तथा $$B$$ का समय $$t=0$$ पर प्रारंभिक कोणीय विस्थापन क्रमशः $$\theta=0$$ तथा $$\theta=\frac{\pi}{2}$$ है।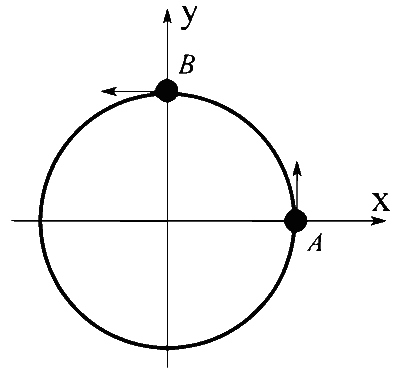	(P)	$${{\sqrt 3 + 1} \over 2}$$
(II)	दो प्रक्षेपणों $$A$$ तथा $$B$$ को क्रमशः $$t=0$$ तथा $$t=0.1 s$$ पर सामान गति $$v=\frac{5 \pi}{\sqrt{2}} \mathrm{~m} \mathrm{~s}^{-1}$$ तथा क्षैतिज समतल से $$45^{\circ}$$ कोण पर प्रेक्षित किया जाता है। $$A$$ तथा $$B$$ की प्रारंभिक दूरी इतनी अधिक है कि उनका टकराव (collision) नहीं होता। $$\left(g=10 \mathrm{~m} \mathrm{~s}^{-2}\right)$$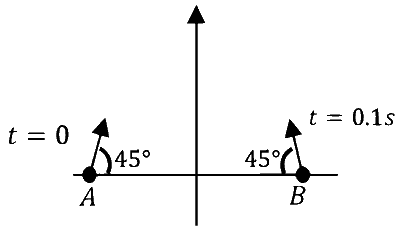	(Q)	$${{(\sqrt 3 - 1)} \over {\sqrt 2 }}$$
(III)	$$t=0$$ से प्रारम्भ हो कर, दो सरल आवृती दोलक $$A$$ तथा $$B$$, $$x$$ दिशा में क्रमशः $$x_{A}=x_{0} \sin \frac{t}{t_{0}}$$ तथा $$x_{B}=x_{0} \sin \left(\frac{t}{t_{0}}+\frac{\pi}{2}\right)$$ के अनुसार गतिमान हैं। $$x_{0}=1 \mathrm{~m}, t_{0}=1 \mathrm{~s}$$ लें.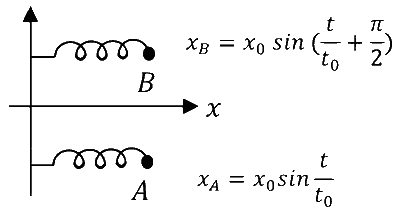	(R)	$$\sqrt {10} $$
(IV)	कण $$A$$ एक समतल $$x y$$ पर $$1 \mathrm{~m}$$ त्रिज्या के क्षैतिज वृतीय पथ पर एकसमान कोणीय गति $$\omega=1 \mathrm{rad} \mathrm{s}^{-1}$$ से घूम रहा है। कण $$B$$ ऊपर की ओर एकसमान गति $$3 \mathrm{~m} \mathrm{~s}^{-1}$$ से उर्ध्वाधर दिशा में गतिमान होता है, जैसा की चित्र में दर्शाया गया है। (गुरुत्व नगण्य है|)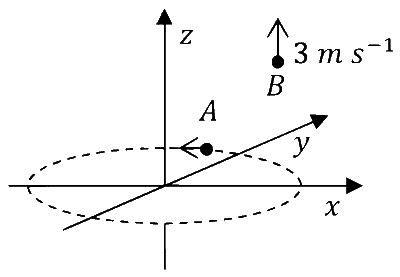	(S)	$$\sqrt 2 $$
		(T)	$$\sqrt {25{\pi ^2} + 1} $$

निम्न में से कौनसा एक विकल्प सही है?

लिस्ट I चार विभिन्न तंत्रों की उष्मागतिकी प्रक्रम (thermodynamic process) को दर्शाता है। लिस्ट II में इस प्रक्रम के कारण आतंरिक उर्जा (internal energy) के परिमाण (या तो परिशुद्ध या निकटतम) में संभावित परिवर्तन दिया गया है|

	सूची-I		सूची-II
(I)	$$10^{-3} \mathrm{~kg}$$ पानी को $$100^{\circ} \mathrm{C}$$ पर इसी तापमान पर भाप में परिवर्तित किया जाता है, दाब $$10^{5} \mathrm{~Pa}$$ है। इस प्रक्रम में आयतन में परिवर्तन $$10^{-6} \mathrm{~m}^{3}$$ से $$10^{-3} \mathrm{~m}^{3}$$ है| पानी की गुप्त उष्मा (latent heat) = $$2250 \mathrm{~kJ} / \mathrm{~kg}$$ है।	(P)	2 kJ
(II)	$$0.2$$ मोल की एक द्रढ़ द्विपरमाणुक (rigid diatomic) आदर्श गैस के $$V$$ आयतन को $$500 \mathrm{~K}$$ तापमान पर सम्दाबीय प्रसारण से $$3 V$$ आयतन में परिवर्तित किया जाता है। मान लें $$R=8.0 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$$.	(Q)	7 kJ
(III)	एक मोल की एकपरमाणुक (monatomic) आदर्श गैस को रुधोस्म (adiabatic) प्रक्रम द्वारा आयतन $$V=\frac{1}{3} m^{3}$$ और दबाव $$2 k P a$$ से आयतन $$\frac{V}{8}$$ में दबाया जाता है।	(R)	4 kJ
(IV)	तीन मोल की द्विपरमाणुक आदर्श गैस, जिसका अणु कम्पित (vibrate) कर सकता है, को 9 $$k J$$ की उष्मा दी गई है और समदाबी प्रसारण करती है।	(S)	5 kJ
		(T)	3 kJ

निम्न में से कौनसा एक विकल्प सही है?

लिस्ट I में दो लेंसों (1 तथा 2) के चार युग्मों (combinations) को दर्शाया गया है जिनकी फोकल दूरी ( $$\mathrm{cm}$$ में) चित्रों में सूचित है| सभी अवस्थाओं में बिंब (object) को पहले लेंस से $$20 \mathrm{~cm}$$ बायीं और रखा है तथा दोनों लेंसों के बीच की दूरी $$5 \mathrm{~cm}$$ है| लिस्ट II में अंतिम प्रतिबिम्ब (image) की स्थितियाँ दी गयी है।

	सूची-I		सूची-II
(I)		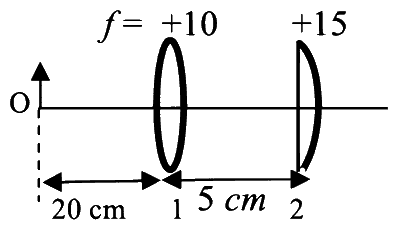(P)	अंतिम प्रतिबिम्ब, लेंस 2 से $$7.5 \mathrm{~cm}$$ दायीं ओर बनता है।
(II)		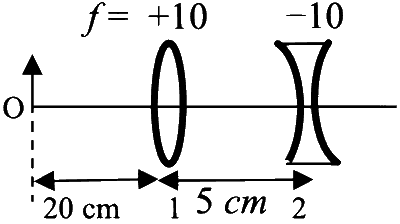(Q)	अंतिम प्रतिबिम्ब, लेंस 2 से $$60.0 \mathrm{~cm}$$ दायीं ओर बनता है।
(III)		(R)	अंतिम प्रतिबिम्ब, लेंस 2 से $$30.0 \mathrm{~cm}$$ बायीं ओर बनता है।
(IV)		(S)	अंतिम प्रतिबिम्ब, लेंस 2 से $$6.0 \mathrm{~cm}$$ दायीं ओर बनता है।
		(T)	अंतिम प्रतिबिम्ब, लेंस 2 से $$30.0 \mathrm{~cm}$$ दायीं ओर बनता है।

निम्न में से कौनसा एक विकल्प सही है?