लिस्ट $$\mathrm{I}$$ में चार तंत्र (system) वर्णित हैं, प्रत्येक में दो कण $$A$$ और $$B$$ की सापेक्ष गति (relative speed) का चित्रण किया गया है| लिस्ट $$\mathrm{II}$$ में उनकी सापेक्ष गति ($$\mathrm{m} \mathrm{s}^{-1}$$ में) का संभावित परिमाण समय $$t=\frac{\pi}{3} s$$ पर दिया गया है।

	सूची-I		सूची-II
(I)	$$A$$ तथा $$B$$ एक $$1 \mathrm{~m}$$ त्रिज्या के वृत पर एकसमान कोणीय गति $$\omega=1 \mathrm{rad} \mathrm{s}^{-1}$$ से घूमते हैं जहाँ $$A$$ तथा $$B$$ का समय $$t=0$$ पर प्रारंभिक कोणीय विस्थापन क्रमशः $$\theta=0$$ तथा $$\theta=\frac{\pi}{2}$$ है।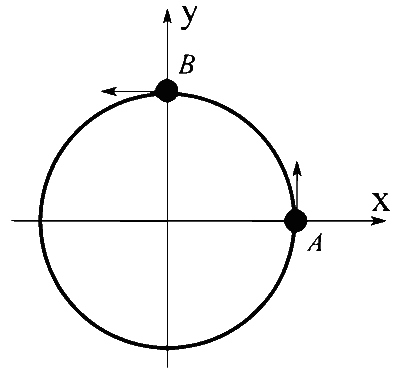	(P)	$${{\sqrt 3 + 1} \over 2}$$
(II)	दो प्रक्षेपणों $$A$$ तथा $$B$$ को क्रमशः $$t=0$$ तथा $$t=0.1 s$$ पर सामान गति $$v=\frac{5 \pi}{\sqrt{2}} \mathrm{~m} \mathrm{~s}^{-1}$$ तथा क्षैतिज समतल से $$45^{\circ}$$ कोण पर प्रेक्षित किया जाता है। $$A$$ तथा $$B$$ की प्रारंभिक दूरी इतनी अधिक है कि उनका टकराव (collision) नहीं होता। $$\left(g=10 \mathrm{~m} \mathrm{~s}^{-2}\right)$$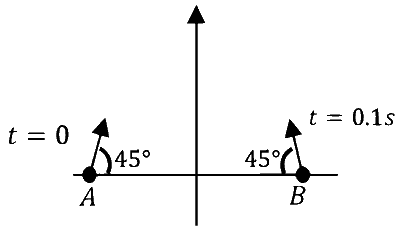	(Q)	$${{(\sqrt 3 - 1)} \over {\sqrt 2 }}$$
(III)	$$t=0$$ से प्रारम्भ हो कर, दो सरल आवृती दोलक $$A$$ तथा $$B$$, $$x$$ दिशा में क्रमशः $$x_{A}=x_{0} \sin \frac{t}{t_{0}}$$ तथा $$x_{B}=x_{0} \sin \left(\frac{t}{t_{0}}+\frac{\pi}{2}\right)$$ के अनुसार गतिमान हैं। $$x_{0}=1 \mathrm{~m}, t_{0}=1 \mathrm{~s}$$ लें.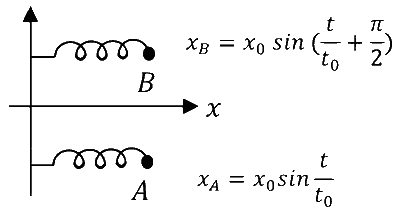	(R)	$$\sqrt {10} $$
(IV)	कण $$A$$ एक समतल $$x y$$ पर $$1 \mathrm{~m}$$ त्रिज्या के क्षैतिज वृतीय पथ पर एकसमान कोणीय गति $$\omega=1 \mathrm{rad} \mathrm{s}^{-1}$$ से घूम रहा है। कण $$B$$ ऊपर की ओर एकसमान गति $$3 \mathrm{~m} \mathrm{~s}^{-1}$$ से उर्ध्वाधर दिशा में गतिमान होता है, जैसा की चित्र में दर्शाया गया है। (गुरुत्व नगण्य है|)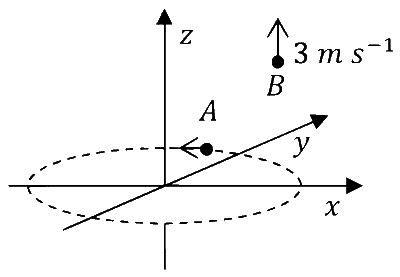	(S)	$$\sqrt 2 $$
		(T)	$$\sqrt {25{\pi ^2} + 1} $$

निम्न में से कौनसा एक विकल्प सही है?