JEE Advance - Physics Hindi (2022 - Paper 1 Online - No. 4)
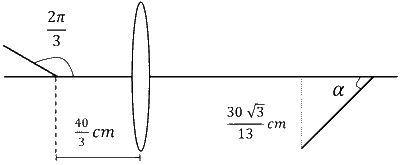
$2 \mathrm{~cm}$ लम्बाई की एक छड़ एक पतले उत्तल लेंस के मुख्य अक्ष के साथ $\frac{2 \pi}{3}$ रेडियन कोण निर्मित करती है। लेंस की फोकस दूरी $10 \mathrm{~cm}$ है तथा इसे चित्र में दर्शाए अनुसार वस्तु से $\frac{40}{3} \mathrm{~cm}$ की दूरी पर रखा जाता है। प्रतिबिम्ब की ऊँचाई $\frac{30 \sqrt{3}}{13} \mathrm{~cm}$ है तथा मुख्य अक्ष के सापेक्ष इसके द्वारा बनाया गया कोण $\alpha$ रेडियन है। $\alpha$ का मान $\frac{\pi}{n}$ रेडियन है, जहाँ $n$ __________ है।
Answer
5.95TO6.05
Explanation
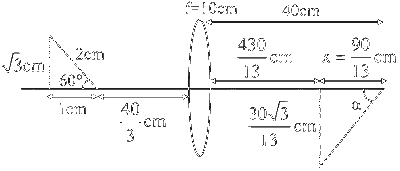
$\frac{\mathrm{h}_{\mathrm{i}}}{\mathrm{h}_0}=\frac{\mathrm{v}}{\mathrm{u}} \Rightarrow \frac{-\frac{30 \sqrt{3}}{13}}{\sqrt{3}}=\frac{\mathrm{v}}{-\frac{43}{3}} \Rightarrow \mathrm{v}_1=\frac{430}{13} \mathrm{~cm}$
Now using,
$ \frac{1}{\mathrm{v}}-\frac{1}{\mathrm{u}}=\frac{1}{\mathrm{f}} \Rightarrow \frac{1}{\mathrm{v}}=\frac{1}{10}-\frac{3}{40} \Rightarrow \mathrm{v}=40 \mathrm{~cm}$
$$ \therefore $$ $ \mathrm{x}=40-\frac{430}{13}=\frac{90}{13} \mathrm{~cm}$
$\tan \alpha=\frac{\frac{30 \sqrt{3}}{\frac{90}{13}}}{\mathrm{~N}}=\frac{1}{\sqrt{3}} \Rightarrow \alpha=30^{\circ}=\frac{\pi}{6}$
$$ \therefore $$ N = 6
Comments (0)


