JEE Advance - Physics Hindi (2022 - Paper 1 Online - No. 9)
एक समान्तर प्लेट संधारित्र की प्लेटों के मध्य अंतराल को परावैद्युतांक $K>1$ वाले एक माध्यम से भरा जाता है। प्लेटों का क्षेत्रफल अत्यधिक है तथा इनके मध्य की दूरी $d$ है। संधारित्र को चित्र (a) में दर्शाए अनुसार वोल्टता $V$ की एक बैटरी से संयोजित किया जाता है। अब दोनों प्लेटों को चित्र (b) में दर्शाए अनुसार इनकी मूल स्थितियों से $\frac{d}{2}$ दूरी तक गति करायी जाती है।
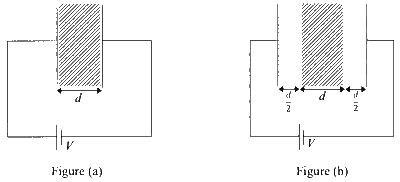
चित्र (a) में तथा चित्र (b) में प्रदर्शित अभिविन्यास से गुजरने वाली प्रक्रिया में, निम्नलिखित में कौनसा / कौनसे कथन सही है / हैं?
Explanation
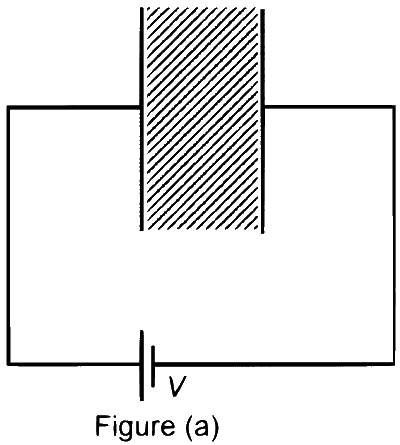
$C_a=\frac{K \varepsilon_0 A}{d}$
$$ \therefore $$ $q_a=\frac{K \varepsilon_0 A}{d} V$
$ E_a =\frac{q_a}{K A \varepsilon_0}$
$=\frac{K \varepsilon_0 A V}{d K \varepsilon_0 A} $
$ =\frac{V}{d}$
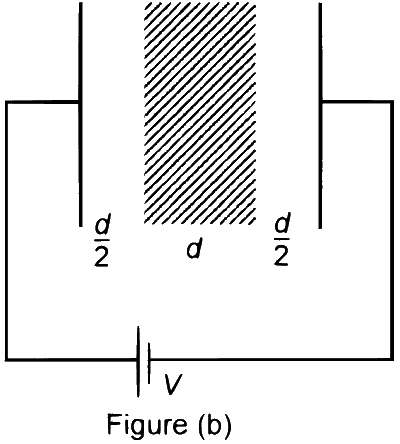
$\begin{aligned} C_b & =\frac{\varepsilon_0 A}{d+\left(\frac{d}{K}\right)} \\\\ & =\frac{\varepsilon_0 A K}{d(K+1)}\end{aligned}$
$q_b=\frac{\varepsilon_0 A K V}{d(K+1)}$
$\left(E_b\right)_{\text {dielectric }} $
$=\frac{E_{\text {air }}}{K} $
$=\frac{q_b}{K A \varepsilon_0} $
$=\frac{\varepsilon_0 A K V}{d(K+1)\left(K A \varepsilon_0\right)}$
$ =\frac{V}{d(K+1)}$
$\begin{aligned} &\therefore\text { Capacitance decrease by a factor of } \frac{1}{K+1} \\\\ & \text { Work done in the process }=U_f-U_i \\\\ &=\frac{1}{2}\left(C_f-C_i\right) V^2 \\\\ &=\frac{1}{2}\left(\frac{\varepsilon_0 A K}{d(K+1)}-\frac{K \varepsilon_0 A}{d}\right) V^2 \\\\ &=\frac{1}{2} V^2 \frac{\varepsilon_0 A K}{d}\left(\frac{1}{K+1}-1\right) \\\\ &=\frac{1}{2} \frac{\varepsilon_0 A K V^2}{d} \frac{1-K-1}{K+1} \\\\ &=\frac{1}{2} \frac{\varepsilon_0 A V^2}{d}\left(\frac{-K^2}{K+1}\right)\end{aligned}$
Comments (0)


