The angle rotated by disc in $t=\sqrt{\pi} \mathrm{s}$ is

$$ \begin{aligned} & \theta=\omega_0 t+\frac{1}{2} \alpha t^2 \\\\ & \Rightarrow \theta=\frac{1}{2} \times \frac{2}{3}(\sqrt{\pi})^2 \\\\ &=\frac{\pi}{3} \mathrm{rad} \end{aligned} $$

and the angular velocity of disc is

$$ \begin{aligned} \omega & =\omega_0+\alpha t \\\\ = & \frac{2 \sqrt{\pi}}{3} \mathrm{rad} / \mathrm{s} \\\\ \text { and } v_{\mathrm{cm}} & =\omega R=\frac{2 \sqrt{\pi}}{3} \times 1 \\\\ & =\frac{2 \sqrt{\pi}}{3} \mathrm{~m} / \mathrm{s} \end{aligned} $$

So, at the moment it detaches the situation is



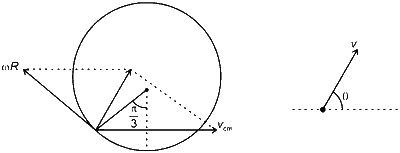
$v=\sqrt{(\omega R)^2+v_{\mathrm{cm}}^2+2(\omega R) v_{\mathrm{cm}} \cos 120^{\circ}}$

$=v_{\mathrm{cm}}=\frac{2 \sqrt{\pi}}{3} \mathrm{~m} / \mathrm{s}$

and $\tan \theta=\frac{\omega R \sin 120^{\circ}}{v_{\mathrm{cm}}+\omega R \cos 120^{\circ}}$

$\Rightarrow \tan \theta=\sqrt{3}$

$\Rightarrow \theta=\frac{\pi}{3} \mathrm{rad}$

So, $H_{\max }=\frac{u^2 \sin ^2 \theta}{2 g}$

$=\frac{\left(\frac{2 \sqrt{\pi}}{3}\right)^2 \times \sin ^2 60^{\circ}}{2 \times 10}$

$$ \begin{aligned} & =\frac{4 \pi \times 3}{9 \times 2 \times 10 \times 4} \\\\ & =\frac{\pi}{60} \mathrm{~m} \end{aligned} $$

So, height from ground will be

$$ = R\left(1-\cos 60^{\circ}\right)+\frac{\pi}{60}=\frac{1}{2}+\frac{x}{10}$$

$$ \Rightarrow x=\frac{\pi}{6}=0.52 $$