JEE Advance - Physics Hindi (2022 - Paper 1 Online - No. 15)
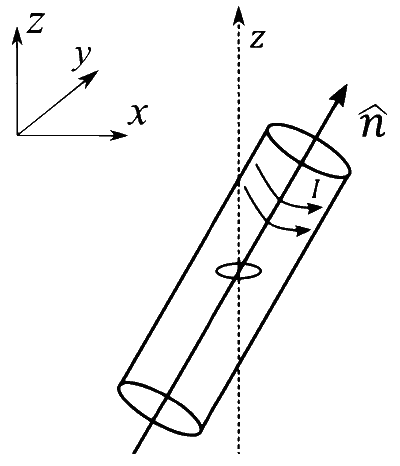
एक छोटा वृतीय छल्ला (circular loop) जिसका क्षेत्रफल $$A$$ तथा प्रतिरोध $$R$$ है, एक क्षैतिज (horizontal) $$x y$$-तल पर नियत किया गया है। छल्ले का केन्द्र हमेशा एक लम्बी परिनलिका (solenoid) के अक्ष $$\hat{n}$$ पर रहता है। इस परिनलिका में $$m$$ घुमाव प्रति मानक लम्बाई (turns per unit length) तथा धारा $$I$$ वामावर्त (anticlockwise) दिशा में हैं, जैसा कि चित्र में दर्शाया गया है। परिनलिका की वजह से चुम्बकीय क्षेत्र $$\hat{n}$$ दिशा में है। लिस्ट I में एकसमान कोणीय आवृति में $$\hat{n}$$ की समय पर आधारिता (dependences) दी गयी है। लिस्ट II में वृतीय छल्ले का बलआघूर्ण (torque) $$t=\frac{\pi}{6 \omega}$$ पर दिया गया है| $$\alpha=\frac{A^{2} \mu_{0}^{2} m^{2} I^{2} \omega}{2 R}$$ लें।
| सूची-I | सूची-II | ||
|---|---|---|---|
| (I) | $$\frac{1}{\sqrt{2}}(\sin \omega t \hat{\jmath}+\cos \omega t \hat{k})$$ | (P) | 0 |
| (II) | $$\frac{1}{\sqrt{2}}(\sin \omega t \hat{\imath}+\cos \omega t \hat{\jmath})$$ | (Q) | $$-\frac{\alpha}{4} \hat{\imath}$$ |
| (III) | $$\frac{1}{\sqrt{2}}(\sin \omega t \hat{\imath}+\cos \omega t \hat{k})$$ | (R) | $$\frac{3 \alpha}{4} \hat{\imath}$$ |
| (IV) | $$\frac{1}{\sqrt{2}}(\cos \omega t \hat{\jmath}+\sin \omega t \hat{k})$$ | (S) | $$\frac{\alpha}{4} \hat{\jmath}$$ |
| (T) | $$-\frac{3 \alpha}{4} \hat{\imath}$$ |
निम्न में से कौन सा एक विकल्प सही है?
$$\mathrm{I}\to \mathrm{Q};\mathrm{II}\to \mathrm{P};\mathrm{III}\to \mathrm{S};\mathrm{IV}\to \mathrm{T}$$
$$\mathrm{I}\to \mathrm{S};\mathrm{II}\to \mathrm{T};\mathrm{III}\to \mathrm{Q};\mathrm{IV}\to \mathrm{P}$$
$$\mathrm{I}\to \mathrm{Q};\mathrm{II}\to \mathrm{P};\mathrm{III}\to \mathrm{S};\mathrm{IV}\to \mathrm{R}$$
$$\mathrm{I}\to \mathrm{T};\mathrm{II}\to \mathrm{Q};\mathrm{III}\to \mathrm{P};\mathrm{IV}\to \mathrm{R}$$
Comments (0)


