Emf induced in the circuit is

$$ |E|=\left|\frac{d \phi}{d t}\right| =\frac{d}{d t}\left(\left(B_0+\beta t\right) A\right) $$

$$ =\beta \times A $$

$$ =0.04 \mathrm{~V} $$

So the circuit can be rearranged as



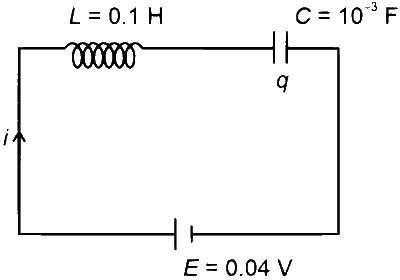
Using Kirchhoff's law we can write

$$ \begin{aligned} & E=L \frac{d i}{d t}+\frac{q}{C} \\\\ & L \frac{d i}{d t}=E-\frac{q}{C} \\\\ & \text { Or } \frac{d^2 q}{d t^2}=-\frac{1}{L C}(q-C E) \end{aligned} $$

Using SHM concept we can write

$$ q=C E+A \sin (\omega t+\phi)\left(\text { where } \omega=\frac{1}{\sqrt{L C}}\right) $$

at $t=0, q=0 \& i=0$

So $A=C E \& \phi=-\frac{\pi}{2}$

$$ q=C E-C E \cos \omega t $$

so $i=\frac{d q}{d t}=C E \omega \sin \omega t$

So,

$$ i_{\max } =\frac{10^{-3} \times 0.04}{\sqrt{0.1 \times 10^{-3}}} $$

$$ =4 \mathrm{~mA} $$