A region in the form of an equilateral triangle (in $x-y$ plane) of height $L$ has a uniform magnetic field $\vec{B}$ pointing in the $+z$-direction. A conducting loop $\mathrm{PQR}$, in the form of an equilateral triangle of the same height $L$, is placed in the $x-y$ plane with its vertex $\mathrm{P}$ at $x=0$ in the orientation shown in the figure. At $t=0$, the loop starts entering the region of the magnetic field with a uniform velocity $\vec{v}$ along the $+x$-direction. The plane of the loop and its orientation remain unchanged throughout its motion.

Which of the following graph best depicts the variation of the induced emf $(E)$ in the loop as a function of the distance $(x)$ starting from $x=0$ ?

A particle of mass $m$ is under the influence of the gravitational field of a body of mass $M(\gg m)$. The particle is moving in a circular orbit of radius $r_0$ with time period $T_0$ around the mass $M$. Then, the particle is subjected to an additional central force, corresponding to the potential energy $V_{\mathrm{c}}(r)=m \alpha / r^3$, where $\alpha$ is a positive constant of suitable dimensions and $r$ is the distance from the center of the orbit. If the particle moves in the same circular orbit of radius $r_0$ in the combined gravitational potential due to $M$ and $V_{\mathrm{c}}(r)$, but with a new time period $T_1$, then $\left(T_1^2-T_0^2\right) / T_1^2$ is given by

[G is the gravitational constant.]

A metal target with atomic number $Z=46$ is bombarded with a high energy electron beam. The emission of X-rays from the target is analyzed. The ratio $r$ of the wavelengths of the $K_\alpha$-line and the cut-off is found to be $r=2$. If the same electron beam bombards another metal target with $Z=41$, the value of $r$ will be

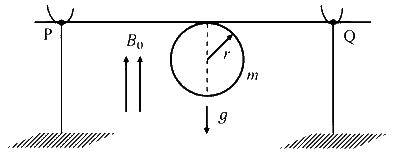
A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass $m$ and radius $r$ and it is in a uniform vertical magnetic field $B_0$, as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity $g$, on two conducting supports at $\mathrm{P}$ and $\mathrm{Q}$. When a current $I$ is passed through the loop, the loop turns about the line $\mathrm{PQ}$ by an angle $\theta$ given by

A small electric dipole $\vec{p}_0$, having a moment of inertia $I$ about its center, is kept at a distance $r$ from the center of a spherical shell of radius $R$. The surface charge density $\sigma$ is uniformly distributed on the spherical shell. The dipole is initially oriented at a small angle $\theta$ as shown in the figure. While staying at a distance $r$, the dipole is free to rotate about its center.

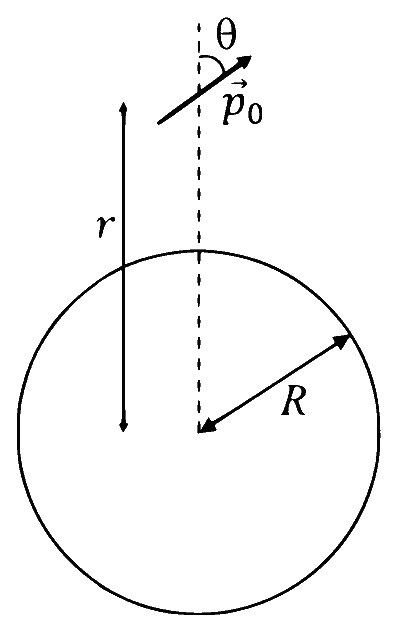
If released from rest, then which of the following statement(s) is(are) correct?

[ $\varepsilon_0$ is the permittivity of free space.]

A table tennis ball has radius $(3 / 2) \times 10^{-2} \mathrm{~m}$ and mass $(22 / 7) \times 10^{-3} \mathrm{~kg}$. It is slowly pushed down into a swimming pool to a depth of $d=0.7 \mathrm{~m}$ below the water surface and then released from rest. It emerges from the water surface at speed $v$, without getting wet, and rises up to a height $H$. Which of the following option(s) is(are) correct?

[Given: $\pi=22 / 7, g=10 \mathrm{~m} \mathrm{~s}^{-2}$, density of water $=1 \times 10^3 \mathrm{~kg} \mathrm{~m}^{-3}$, viscosity of water $=1 \times 10^{-3} \mathrm{~Pa}$-s.]

A positive, singly ionized atom of mass number $A_{\mathrm{M}}$ is accelerated from rest by the voltage $192 \mathrm{~V}$. Thereafter, it enters a rectangular region of width $w$ with magnetic field $\vec{B}_0=0.1 \hat{k}$ Tesla, as shown in the figure. The ion finally hits a detector at the distance $x$ below its starting trajectory.

[Given: Mass of neutron/proton $=(5 / 3) \times 10^{-27} \mathrm{~kg}$, charge of the electron $=1.6 \times 10^{-19} \mathrm{C}$.]

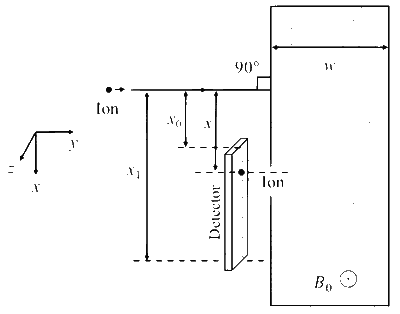
Which of the following option(s) is(are) correct?

The dimensions of a cone are measured using a scale with a least count of $2 \mathrm{~mm}$. The diameter of the base and the height are both measured to be $20.0 \mathrm{~cm}$. The maximum percentage error in the determination of the volume is _______.

A ball is thrown from the location $\left(x_0, y_0\right)=(0,0)$ of a horizontal playground with an initial speed $v_0$ at an angle $\theta_0$ from the $+x$-direction. The ball is to be hit by a stone, which is thrown at the same time from the location $\left(x_1, y_1\right)=(L, 0)$. The stone is thrown at an angle $\left(180-\theta_1\right)$ from the $+x$-direction with a suitable initial speed. For a fixed $v_0$, when $\left(\theta_0, \theta_1\right)=\left(45^{\circ}, 45^{\circ}\right)$, the stone hits the ball after time $T_1$, and when $\left(\theta_0, \theta_1\right)=\left(60^{\circ}, 30^{\circ}\right)$, it hits the ball after time $T_2$. In such a case, $\left(T_1 / T_2\right)^2$ is ______.

A charge is kept at the central point $\mathrm{P}$ of a cylindrical region. The two edges subtend a half-angle $\theta$ at $\mathrm{P}$, as shown in the figure. When $\theta=30^{\circ}$, then the electric flux through the curved surface of the cylinder is $\Phi$. If $\theta=60^{\circ}$, then the electric flux through the curved surface becomes $\Phi / \sqrt{n}$, where the value of $n$ is ___.

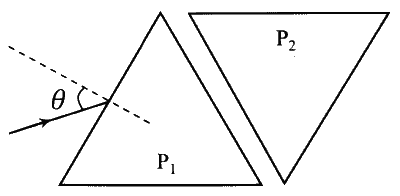
Two equilateral-triangular prisms $\mathrm{P}_1$ and $\mathrm{P}_2$ are kept with their sides parallel to each other, in vacuum, as shown in the figure. A light ray enters prism $\mathrm{P}_1$ at an angle of incidence $\theta$ such that the outgoing ray undergoes minimum deviation in prism $\mathrm{P}_2$. If the respective refractive indices of $\mathrm{P}_1$ and $\mathrm{P}_2$ are $\sqrt{\frac{3}{2}}$ and $\sqrt{3}$, then $\theta=\sin ^{-1}\left[\sqrt{\frac{3}{2}} \sin \left(\frac{\pi}{\beta}\right)\right]$, where the value of $\beta$ is ____.

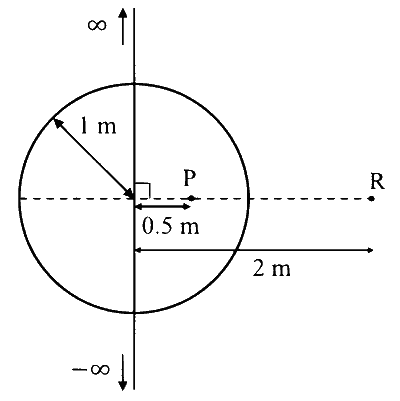
An infinitely long thin wire, having a uniform charge density per unit length of $5 \mathrm{nC} / \mathrm{m}$, is passing through a spherical shell of radius $1 \mathrm{~m}$, as shown in the figure. A $10 \mathrm{nC}$ charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points $\mathrm{P}$ and $\mathrm{R}$, in Volt, is ________.

[Given: In SI units $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9, \ln 2=0.7$. Ignore the area pierced by the wire.]

A spherical soap bubble inside an air chamber at pressure $P_0=10^5 \mathrm{~Pa}$ has a certain radius so that the excess pressure inside the bubble is $\Delta P=144 \mathrm{~Pa}$. Now, the chamber pressure is reduced to $8 P_0 / 27$ so that the bubble radius and its excess pressure change. In this process, all the temperatures remain unchanged. Assume air to be an ideal gas and the excess pressure $\Delta P$ in both the cases to be much smaller than the chamber pressure. The new excess pressure $\Delta P$ in $\mathrm{Pa}$ is ______.

The $8^{\text {th }}$ bright fringe above the point $\mathrm{O}$ oscillates with time between two extreme positions. The separation between these two extreme positions, in micrometer $(\mu \mathrm{m})$, is _________ .

The maximum speed in $\mu \mathrm{m} / \mathrm{s}$ at which the $8^{\text {th }}$ bright fringe will move is ______.

If the collision occurs at time $t_0=0$, the value of $v_{\mathrm{cm}} /(a \omega)$ will be ______.

If the collision occurs at time $t_0=\pi /(2 \omega)$, then the value of $4 b^2 / a^2$ will be ______.