JEE Advance - Physics (2024 - Paper 2 Online - No. 11)
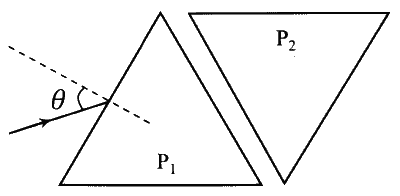
Two equilateral-triangular prisms $\mathrm{P}_1$ and $\mathrm{P}_2$ are kept with their sides parallel to each other, in vacuum, as shown in the figure. A light ray enters prism $\mathrm{P}_1$ at an angle of incidence $\theta$ such that the outgoing ray undergoes minimum deviation in prism $\mathrm{P}_2$. If the respective refractive indices of $\mathrm{P}_1$ and $\mathrm{P}_2$ are $\sqrt{\frac{3}{2}}$ and $\sqrt{3}$, then $\theta=\sin ^{-1}\left[\sqrt{\frac{3}{2}} \sin \left(\frac{\pi}{\beta}\right)\right]$, where the value of $\beta$ is ____.
Explanation
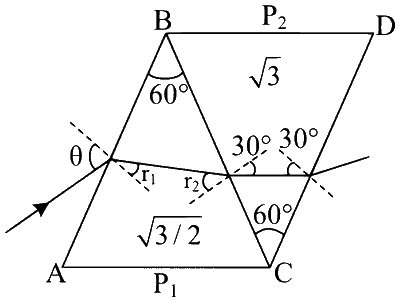
At surface BC
$$\begin{aligned} & \sqrt{\frac{3}{2}} \sin r_2=\sqrt{3} \sin 30 \\ & \sqrt{\frac{3}{2}} \sin r_2=\frac{\sqrt{3}}{2} \\ & \operatorname{sinr}_2=\frac{1}{\sqrt{2}} \\ & r_2=45^{\circ} \\ & r_1=60^{\circ}-45^{\circ}=15^{\circ} \end{aligned}$$
At surface $$A B$$
$$\begin{gathered} 1 \sin \theta=\sqrt{\frac{3}{2}} \sin 15^{\circ} \\ \theta=\sin ^{-1}\left[\sqrt{\frac{3}{2}} \sin \frac{\pi}{12}\right] \\ \beta=12 \end{gathered}$$
Comments (0)


