JEE Advance - Physics (2024 - Paper 2 Online - No. 7)
A positive, singly ionized atom of mass number $A_{\mathrm{M}}$ is accelerated from rest by the voltage $192 \mathrm{~V}$. Thereafter, it enters a rectangular region of width $w$ with magnetic field $\vec{B}_0=0.1 \hat{k}$ Tesla, as shown in the figure. The ion finally hits a detector at the distance $x$ below its starting trajectory.
[Given: Mass of neutron/proton $=(5 / 3) \times 10^{-27} \mathrm{~kg}$, charge of the electron $=1.6 \times 10^{-19} \mathrm{C}$.]
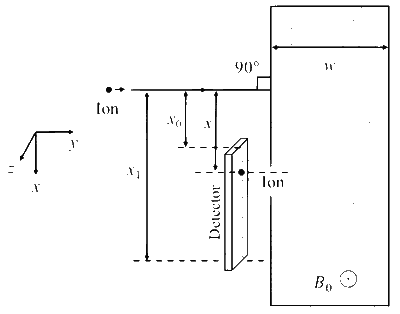
Which of the following option(s) is(are) correct?
Explanation
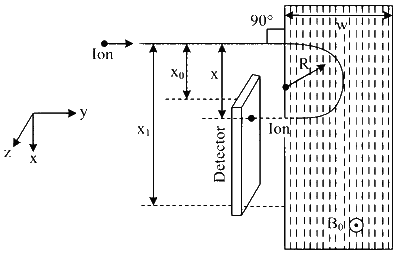
$$\begin{aligned} & x=2 R \\ & \Rightarrow x=2 \frac{P}{q B} \Rightarrow x=\frac{2 \sqrt{2 m q V}}{q B} \Rightarrow x=\frac{2}{B} \sqrt{\frac{2 m V}{q}} \end{aligned}$$
Option A
For $$\mathrm{H}^{+} \rightarrow \mathrm{m}=\frac{5}{3} \times 10^{-27} \mathrm{~kg}$$
$$\therefore x=\frac{2}{0.1} \sqrt{\frac{2 \times \frac{5}{3} \times 10^{-27} \times 192}{1.6 \times 10^{-19}}}=4 \mathrm{~cm}$$
Option B
For $$\mathrm{A}_{\mathrm{m}}=144$$
$$x=\frac{2}{0.1} \sqrt{\frac{2 \times 144 \times \frac{5}{3} \times 10^{-27} \times 192}{1.6 \times 10^{-19}}}=48 \mathrm{~cm}$$
Option C
for $$\mathrm{A}_{\mathrm{m}}=1$$
$$\mathrm{x}=4 \mathrm{~cm}$$ & for $$\mathrm{A}_{\mathrm{m}}=196$$
$$\mathrm{x}=56 \mathrm{~cm}$$.
so $$\mathrm{x}_0=4 \mathrm{~cm}$$ & $$\mathrm{x}_1=56 \mathrm{~cm}$$
$$\therefore \mathrm{x}_1-\mathrm{x}_0=52 \mathrm{~cm}$$.
Option D
Minimum width $$=\mathrm{R}$$
for $$\mathrm{A}_M=196$$
$$\mathrm{R}=\frac{\mathrm{P}}{\mathrm{qB}}=\frac{\sqrt{2 \mathrm{mqV}}}{\mathrm{qB}}$$
$$\mathrm{R}=\frac{1}{\mathrm{~B}} \sqrt{\frac{2 \mathrm{mV}}{\mathrm{q}}}$$
$$\mathrm{w}_{\min }=\mathrm{R}=\frac{1}{0.1} \sqrt{\frac{2 \times 196 \times \frac{5}{3} \times 10^{-27} \times 192}{1.6 \times 10^{-19}}}=28 \mathrm{~cm}$$
Comments (0)


