JEE Advance - Physics (2024 - Paper 2 Online - No. 12)
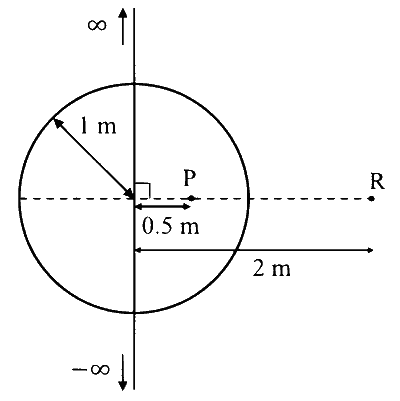
An infinitely long thin wire, having a uniform charge density per unit length of $5 \mathrm{nC} / \mathrm{m}$, is passing through a spherical shell of radius $1 \mathrm{~m}$, as shown in the figure. A $10 \mathrm{nC}$ charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points $\mathrm{P}$ and $\mathrm{R}$, in Volt, is ________.
[Given: In SI units $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9, \ln 2=0.7$. Ignore the area pierced by the wire.]
Explanation
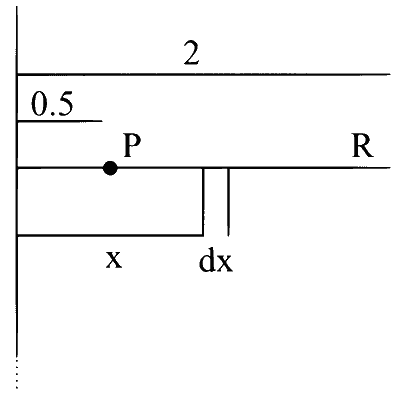
due to wire
$$\begin{aligned} & \mathrm{dV}=-\overrightarrow{\mathrm{E}} \cdot \overrightarrow{\mathrm{dx}} \\ & \int_\limits{\mathrm{v}_{\mathrm{P}}}^{\mathrm{v}_{\mathrm{R}}} \mathrm{dV}=-\int_\limits{0.5}^2 \frac{2 \mathrm{k} \lambda}{\mathrm{x}} \mathrm{dx} \\ & \mathrm{v}_{\mathrm{R}}-\mathrm{v}_{\mathrm{P}}=-2 \mathrm{k} \lambda \ln \frac{2}{0.5} \\ & =-2 \times 9 \times 10^9 \times 3 \times 10^{-9} \times 2 \times 0.7=-126 \mathrm{~V} \end{aligned}$$
due to sphere
$$\begin{aligned} & v_R-v_P= \frac{k Q}{2}-\frac{k Q}{1}=-\frac{k Q}{2}=\frac{-9 \times 10^9 \times 10 \times 10^{-9}}{2} \\ &=-45 \mathrm{~V} \\ & v_R-v_P=-126-45=-171 \mathrm{~V} \\ & v_P-v_R= 171 \mathrm{~V} \end{aligned}$$
Comments (0)


