JEE Advance - Physics (2024 - Paper 2 Online - No. 10)
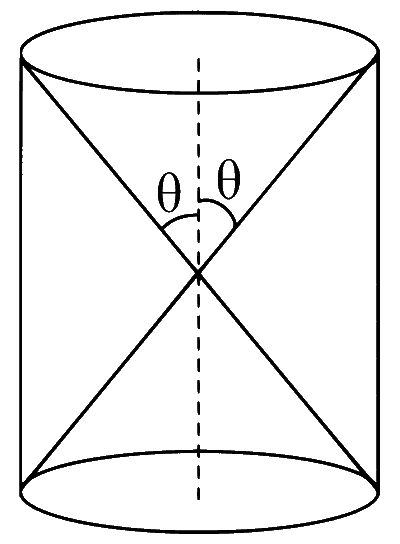
A charge is kept at the central point $\mathrm{P}$ of a cylindrical region. The two edges subtend a half-angle $\theta$ at $\mathrm{P}$, as shown in the figure. When $\theta=30^{\circ}$, then the electric flux through the curved surface of the cylinder is $\Phi$. If $\theta=60^{\circ}$, then the electric flux through the curved surface becomes $\Phi / \sqrt{n}$, where the value of $n$ is ___.

Explanation
Solid angle made by plane surfaces $$\Omega=2 \times 2 \pi(1-\cos \theta)$$
$$\Rightarrow \Omega=4 \pi-4 \pi \cos \theta$$
So solid angle made by curved surface $$=4 \pi-\Omega$$
$$\begin{aligned} & =4 \pi-(4 \pi-4 \pi \cos \theta)=4 \pi \cos \theta \\ & \phi_{30^{\circ}}=\phi=\frac{4 \pi \cos 30^{\circ}}{4 \pi} \frac{\mathrm{Q}}{\epsilon_0}=\cos 30^{\circ} \frac{\mathrm{Q}}{\epsilon_0} \\ & \phi_{60}=\frac{4 \pi \cos 60^{\circ}}{4 \pi} \frac{\mathrm{Q}}{\epsilon_0}=\cos 60^{\circ} \frac{\mathrm{Q}}{\epsilon_0} \\ & \frac{\phi_{30}}{\phi_{60}}=\frac{\cos 30^{\circ}}{\cos 60^{\circ}}=\sqrt{3} \\ & \frac{\phi}{\phi_{60}}=\sqrt{3} \\ & \phi_{60}=\frac{\phi}{\sqrt{3}} \Rightarrow \mathrm{n}=3 \end{aligned}$$
Comments (0)


