JEE Advance - Physics (2024 - Paper 2 Online - No. 4)
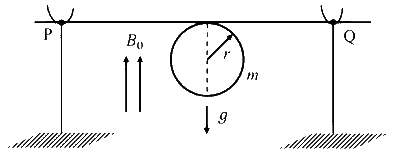
A thin stiff insulated metal wire is bent into a circular loop with its two ends extending tangentially from the same point of the loop. The wire loop has mass $m$ and radius $r$ and it is in a uniform vertical magnetic field $B_0$, as shown in the figure. Initially, it hangs vertically downwards, because of acceleration due to gravity $g$, on two conducting supports at $\mathrm{P}$ and $\mathrm{Q}$. When a current $I$ is passed through the loop, the loop turns about the line $\mathrm{PQ}$ by an angle $\theta$ given by
Explanation
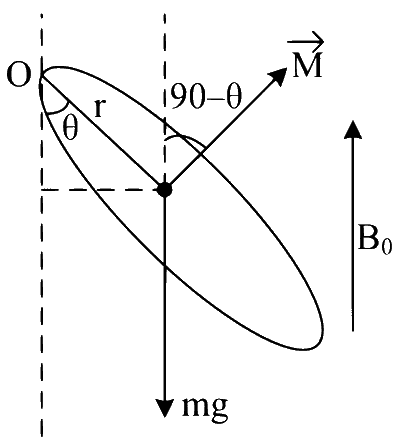
Let loop makes angle $$\theta$$ with vertical.
in equilibrium $$\tau_{\text {net }}=0$$
$$\tau_0=\mathrm{MB} \sin (90-\theta)-\mathrm{mg} . \mathrm{r} \sin \theta=0$$
$$\mathrm{I}$$. $$\pi \mathrm{r}^2 \cdot \mathrm{B}_0 \cos \theta=\mathrm{mg} \mathrm{r} \cdot \sin \theta$$
$$\tan \theta=\frac{\pi \mathrm{rIB}_0}{\mathrm{mg}}$$
Comments (0)


