Sign In

JEE Advance - Physics (2024 - Paper 2 Online - No. 13)

A spherical soap bubble inside an air chamber at pressure $P_0=10^5 \mathrm{~Pa}$ has a certain radius so that the excess pressure inside the bubble is $\Delta P=144 \mathrm{~Pa}$. Now, the chamber pressure is reduced to $8 P_0 / 27$ so that the bubble radius and its excess pressure change. In this process, all the temperatures remain unchanged. Assume air to be an ideal gas and the excess pressure $\Delta P$ in both the cases to be much smaller than the chamber pressure. The new excess pressure $\Delta P$ in $\mathrm{Pa}$ is ______.
Answer
96

Explanation

Case - 1

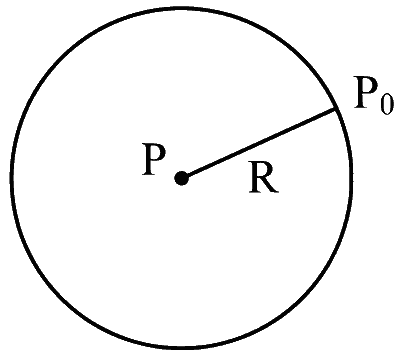
JEE Advanced 2024 Paper 2 Online Physics - Heat and Thermodynamics Question 1 English Explanation 1

$$\begin{aligned} & P-P_0=\Delta P=\frac{4 T}{R} \\ & P=\left(P_0+\frac{4 T}{R}\right) \end{aligned}$$

Case-2

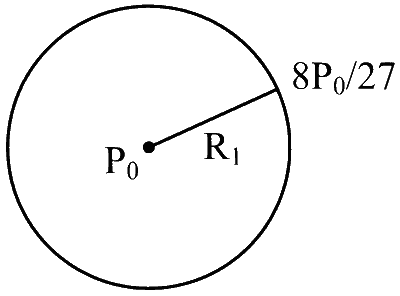
JEE Advanced 2024 Paper 2 Online Physics - Heat and Thermodynamics Question 1 English Explanation 2

$$\begin{aligned} & \mathrm{P}_1-\frac{8 \mathrm{P}_0}{27}=\Delta \mathrm{P}_1=\frac{4 \mathrm{~T}}{\mathrm{R}_1} \\ & \mathrm{P}_1=\frac{4 \mathrm{~T}}{\mathrm{R}_1}+\frac{8 \mathrm{P}_0}{27} \end{aligned}$$

Constant temperature process

$$\begin{aligned} & \mathrm{PV}=\mathrm{P}_1 \mathrm{~V}_1 \\ & \left(\mathrm{P}_0+\frac{4 \mathrm{~T}}{\mathrm{R}}\right) \frac{4}{3} \pi \mathrm{R}^3=\left(\frac{4 \mathrm{~T}}{\mathrm{R}_1}+\frac{8 \mathrm{P}_0}{27}\right) \frac{4}{3} \pi \mathrm{R}_1^3 ;\left(\frac{4 \mathrm{~T}}{\mathrm{R}}\right),\left(\frac{4 \mathrm{~T}}{\mathrm{R}_1}\right) \rightarrow \text { (Neglected) } \\ & \mathrm{R}=\frac{2}{3} \mathrm{R}_1 \Rightarrow \mathrm{R}_1=\frac{3}{2} \mathrm{R} \\ & \Delta \mathrm{P}_1=\frac{4 \mathrm{~T}}{\mathrm{R}_1}=\frac{4 \mathrm{~T}}{3 \mathrm{R}} \times 2=\frac{2}{3} \times(144)=96 \mathrm{~Pa} \end{aligned}$$

Comments (0)

Advertisement