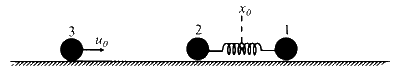
JEE Advance - Physics (2024 - Paper 2 Online - No. 17)
If the collision occurs at time $t_0=\pi /(2 \omega)$, then the value of $4 b^2 / a^2$ will be ______.
Answer
4.25
Explanation
$$\mathrm{t}_0=\frac{\pi}{2 \omega}=\frac{\mathrm{T}}{4}$$
Particles are at extreme position

After collision

in C-frame
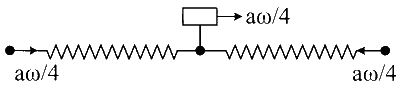
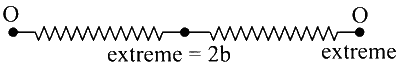
using WET,
$$\begin{aligned} & \mathrm{W}_{\text {spring }}=\Delta \mathrm{K} \\ & \frac{1}{2} \mathrm{k}(2 \mathrm{~b})^2-\frac{1}{2} \mathrm{k}(2 \mathrm{a})^2=2 \times \frac{1}{2} \mathrm{~m} \times\left(\frac{\mathrm{a} \omega}{4}\right)^2 \quad(\mathrm{k}=\text { spring constant }) \\ & 4 \mathrm{~kb}^2-4 \mathrm{ka}^2=2 \times \mathrm{m} \times \frac{\mathrm{a}^2}{16} \times \frac{2 \mathrm{k}}{\mathrm{m}} \\ & 4 \mathrm{~b}^2=\frac{17}{4} \mathrm{a}^2 \\ & \frac{4 \mathrm{~b}^2}{\mathrm{a}^2}=4.25 \end{aligned}$$
Comments (0)