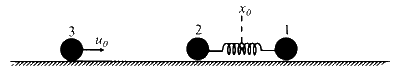
JEE Advance - Physics (2024 - Paper 2 Online - No. 16)
If the collision occurs at time $t_0=0$, the value of $v_{\mathrm{cm}} /(a \omega)$ will be ______.
Answer
0.75
Explanation
At T t$$_0$$ = 0
Before collision

After collision
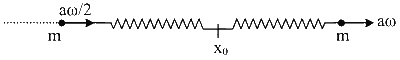
$$\begin{aligned} \mathrm{v}_{\mathrm{CM}} & =\frac{\mathrm{m} \cdot \frac{\mathrm{a} \omega}{2}+\mathrm{m} \cdot \mathrm{a} \omega}{\mathrm{m}+\mathrm{m}} \\ \mathrm{v}_{\mathrm{CM}} & =\frac{3 \mathrm{a} \omega}{4} \\ \frac{\mathrm{V}_{\mathrm{CM}}}{\mathrm{a} \omega} & =\frac{3}{4} \\ \frac{\mathrm{V}_{\mathrm{CM}}}{\mathrm{a} \omega} & =0.75 \end{aligned}$$
Comments (0)