Sign In

JEE Advance - Physics (2024 - Paper 2 Online - No. 9)

A ball is thrown from the location $\left(x_0, y_0\right)=(0,0)$ of a horizontal playground with an initial speed $v_0$ at an angle $\theta_0$ from the $+x$-direction. The ball is to be hit by a stone, which is thrown at the same time from the location $\left(x_1, y_1\right)=(L, 0)$. The stone is thrown at an angle $\left(180-\theta_1\right)$ from the $+x$-direction with a suitable initial speed. For a fixed $v_0$, when $\left(\theta_0, \theta_1\right)=\left(45^{\circ}, 45^{\circ}\right)$, the stone hits the ball after time $T_1$, and when $\left(\theta_0, \theta_1\right)=\left(60^{\circ}, 30^{\circ}\right)$, it hits the ball after time $T_2$. In such a case, $\left(T_1 / T_2\right)^2$ is ______.
Answer
2

Explanation

For Case I :

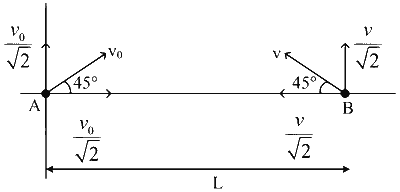
JEE Advanced 2024 Paper 2 Online Physics - Motion Question 1 English Explanation 1

$$\mathrm{a}_{\mathrm{rel}}=0$$

For collision $$\frac{\mathrm{v}_0}{\sqrt{2}}=\frac{\mathrm{v}}{\sqrt{2}}$$

$$\begin{aligned} & \therefore \mathrm{v}=\mathrm{v}_0 \\ & \text { So } \mathrm{T}_1=\frac{\mathrm{L}}{\frac{\mathrm{v}_0}{\sqrt{2}}+\frac{\mathrm{v}}{\sqrt{2}}} \\ & \therefore \tau_1=\frac{\mathrm{L}}{\sqrt{2} \mathrm{v}_0} \quad \text{... (1)} \end{aligned}$$

For case II,

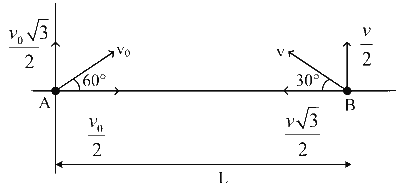
JEE Advanced 2024 Paper 2 Online Physics - Motion Question 1 English Explanation 2

$$\mathrm{a}_{\mathrm{rel}}=0$$

For collision, $$\frac{v_0 \sqrt{3}}{2}=\frac{v}{2}$$

$$\begin{aligned} & \therefore \mathrm{v}=\sqrt{3} \mathrm{v}_0 \\ & \text { So, } \mathrm{T}_2=\frac{\mathrm{L}}{\frac{\mathrm{v}_0}{2}+\mathrm{v} \frac{\sqrt{3}}{2}} \\ & \mathrm{~T}_2=\frac{\mathrm{L}}{\frac{\mathrm{v}_0}{2}+\frac{3 \mathrm{v}_0}{2}} \\ & \therefore \mathrm{T}_2=\frac{\mathrm{L}}{2 \mathrm{v}_0} \quad \ldots . .(2) \\ & \text { so, }\left(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right)^2=(\sqrt{2})^2=2 \Rightarrow\left(\frac{\mathrm{T}_1}{\mathrm{~T}_2}\right)^2=2 \end{aligned}$$

Comments (0)

Advertisement