JEE Advance - Physics (2024 - Paper 2 Online - No. 1)
A region in the form of an equilateral triangle (in $x-y$ plane) of height $L$ has a uniform magnetic field $\vec{B}$ pointing in the $+z$-direction. A conducting loop $\mathrm{PQR}$, in the form of an equilateral triangle of the same height $L$, is placed in the $x-y$ plane with its vertex $\mathrm{P}$ at $x=0$ in the orientation shown in the figure. At $t=0$, the loop starts entering the region of the magnetic field with a uniform velocity $\vec{v}$ along the $+x$-direction. The plane of the loop and its orientation remain unchanged throughout its motion.

Which of the following graph best depicts the variation of the induced emf $(E)$ in the loop as a function of the distance $(x)$ starting from $x=0$ ?

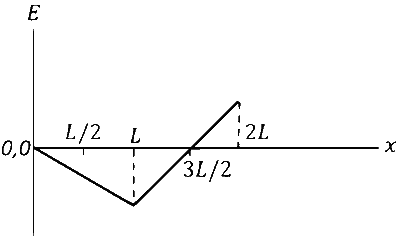
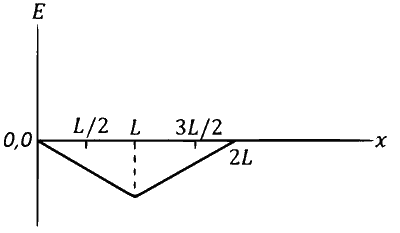
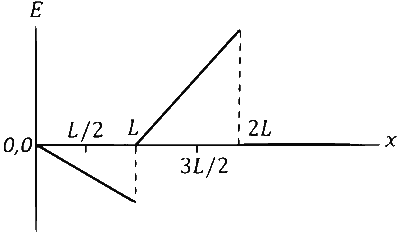
Explanation
0 to L
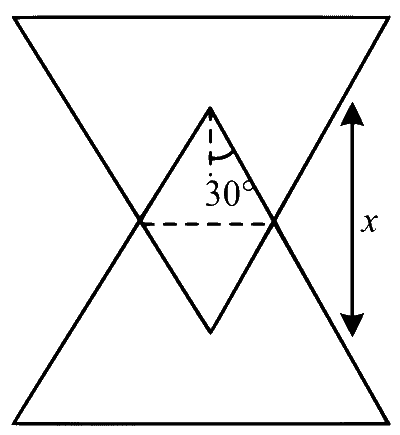
$$\varepsilon=\mathrm{B} \ell_{\mathrm{ent}} \mathrm{v}=\mathrm{B} \times \frac{\mathrm{x}}{\sqrt{3}} \mathrm{v}$$
L to 2 L
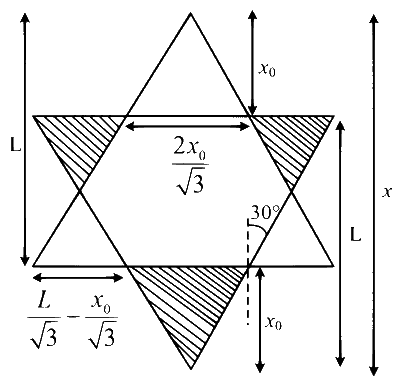
$$\begin{aligned} & |\operatorname{emf}|=B\left(\frac{L}{\sqrt{3}}-\frac{x_0}{\sqrt{3}}\right) v-B \frac{2 x_0}{\sqrt{3}} v \\ & =\frac{B v L}{\sqrt{3}}-\sqrt{3} B v x_0 \\ & =B v\left[\frac{L}{\sqrt{3}}-\sqrt{3}(x-L)\right] \\ & =\frac{B v}{\sqrt{3}}[L-3 x+3 L] \\ & =\frac{B v}{\sqrt{3}}[4 L-3 x] \\ & \text { at } x=\frac{4 L}{3} \\ & \text { emf }=0 \end{aligned}$$
Comments (0)


