Sign In

JEE Advance - Physics (2024 - Paper 2 Online - No. 5)

A small electric dipole $\vec{p}_0$, having a moment of inertia $I$ about its center, is kept at a distance $r$ from the center of a spherical shell of radius $R$. The surface charge density $\sigma$ is uniformly distributed on the spherical shell. The dipole is initially oriented at a small angle $\theta$ as shown in the figure. While staying at a distance $r$, the dipole is free to rotate about its center.

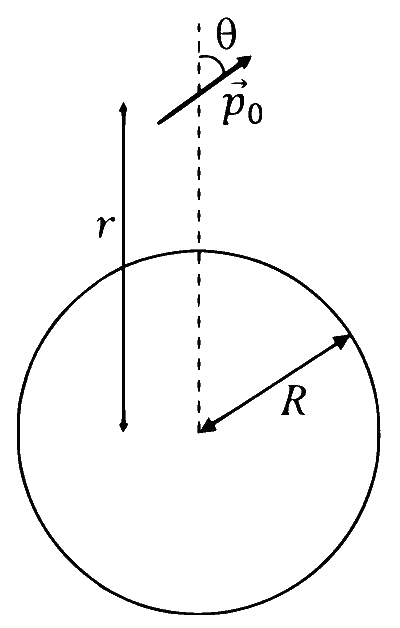
JEE Advanced 2024 Paper 2 Online Physics - Electrostatics Question 3 English

If released from rest, then which of the following statement(s) is(are) correct?

[ $\varepsilon_0$ is the permittivity of free space.]

The dipole will undergo small oscillations at any finite value of $r$.
The dipole will undergo small oscillations at any finite value of $r>R$.
The dipole will undergo small oscillations with an angular frequency of $\sqrt{\frac{2 \sigma p_0}{\epsilon_0 I}}$ at $r=2 R$.
The dipole will undergo small oscillations with an angular frequency of $\sqrt{\frac{\sigma p_0}{100 \epsilon_0 I}}$ at $r=10 R$.

Explanation

The electric field inside sphere is zero. So dipole will oscillate when $$r>R$$.

$$\begin{aligned} & \text { For } \mathrm{r}>\mathrm{RE}=\frac{\sigma \mathrm{R}^2}{\varepsilon_0 \mathrm{r}^2} \\ & \omega=\sqrt{\frac{\mathrm{PE}}{\mathrm{I}}}=\sqrt{\frac{\mathrm{P}_0 \sigma \mathrm{R}^2}{\mathrm{I} \varepsilon_0 \mathrm{r}^2}} \end{aligned}$$

when $$r=2 R$$

$$\omega=\sqrt{\frac{\mathrm{P}_0 \sigma}{4 \mathrm{I} \varepsilon_0}}$$

when $$r=10 R$$

$$\omega=\sqrt{\frac{\mathrm{P}_0 \sigma}{100 \mathrm{I} \varepsilon_0}}$$

Comments (0)

Advertisement