Sign In

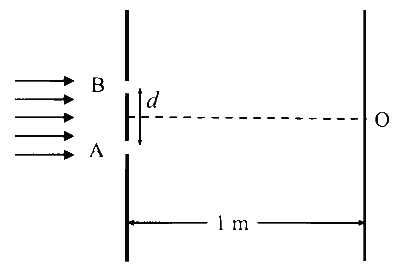
JEE Advance - Physics (2024 - Paper 2 Online - No. 15)

In a Young's double slit experiment, each of the two slits A and B, as shown in the figure, are oscillating about their fixed center and with a mean separation of $0.8 \mathrm{~mm}$. The distance between the slits at time $t$ is given by $d=(0.8+0.04 \sin \omega t) \mathrm{mm}$, where $\omega=0.08 \mathrm{rad} \mathrm{s}^{-1}$. The distance of the screen from the slits is $1 \mathrm{~m}$ and the wavelength of the light used to illuminate the slits is $6000$ Å . The interference pattern on the screen changes with time, while the central bright fringe (zeroth fringe) remains fixed at point $O$.

In a Young's double slit experiment, each of the two slits A and B, as shown in the figure, are oscillating about their fixed center and with a mean separation of $0.8 \mathrm{~mm}$. The distance between the slits at time $t$ is given by $d=(0.8+0.04 \sin \omega t) \mathrm{mm}$, where $\omega=0.08 \mathrm{rad} \mathrm{s}^{-1}$. The distance of the screen from the slits is $1 \mathrm{~m}$ and the wavelength of the light used to illuminate the slits is $6000$ Å . The interference pattern on the screen changes with time, while the central bright fringe (zeroth fringe) remains fixed at point $O$.

In a Young's double slit experiment, each of the two slits A and B, as shown in the figure, are oscillating about their fixed center and with a mean separation of $0.8 \mathrm{~mm}$. The distance between the slits at time $t$ is given by $d=(0.8+0.04 \sin \omega t) \mathrm{mm}$, where $\omega=0.08 \mathrm{rad} \mathrm{s}^{-1}$. The distance of the screen from the slits is $1 \mathrm{~m}$ and the wavelength of the light used to illuminate the slits is $6000$ Å . The interference pattern on the screen changes with time, while the central bright fringe (zeroth fringe) remains fixed at point $O$.

The maximum speed in $\mu \mathrm{m} / \mathrm{s}$ at which the $8^{\text {th }}$ bright fringe will move is ______.
Answer
24

Explanation

$$\begin{aligned} & \mathrm{y}=\mathrm{n} \cdot \frac{\lambda \mathrm{D}}{\mathrm{d}} \\ & \mathrm{v}=\frac{\mathrm{dy}}{\mathrm{dt}}=-\mathrm{n} \cdot \frac{\lambda \cdot \mathrm{d}}{\mathrm{d}^2} \cdot \frac{\mathrm{d}(\mathrm{d})}{\mathrm{dt}} \\ & \mathrm{d}=0.8+0.04 \sin \omega \mathrm{t} \\ & \frac{\mathrm{d}(\mathrm{d})}{\mathrm{dt}}=0.04 \omega \cos \omega \mathrm{t} \\ & \text { for } \mathrm{v} \rightarrow \max \Rightarrow \frac{\mathrm{d}(\mathrm{d})}{\mathrm{dt}} \rightarrow \max \\ & \text { For } \frac{\mathrm{d}(\mathrm{d})}{\mathrm{dt}} \rightarrow \max \\ & \cos \omega \mathrm{t}=1 \Rightarrow \sin \omega \mathrm{t}=0 \\ & \Rightarrow\left(\frac{\mathrm{d}(\mathrm{d})}{\mathrm{dt}}\right)_{\max }=0.04 \\ & \Rightarrow \mathrm{d}=0.8 \mathrm{~mm} \\ & \mathrm{v}_{\max }=\frac{8 \times 6000 \times 10^{-10} \times 1 \times 0.04 \times 0.08}{0.8 \times 0.8 \times 10^{-6} \times 10^{-3}}=24 \mu \mathrm{m} / \mathrm{s} \end{aligned}$$

Comments (0)

Advertisement