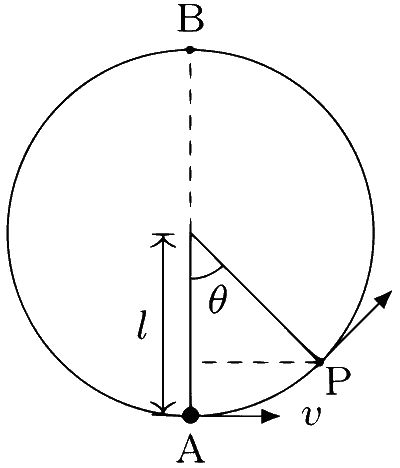
JEE Advance - Physics (2008 - Paper 2 Offline)
STATEMENT-2: If the observer and the object are moving at velocities $${\overrightarrow v _1}$$ and $${\overrightarrow v _2}$$ respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is $${\overrightarrow v _2}$$ - $${\overrightarrow v _1}$$.
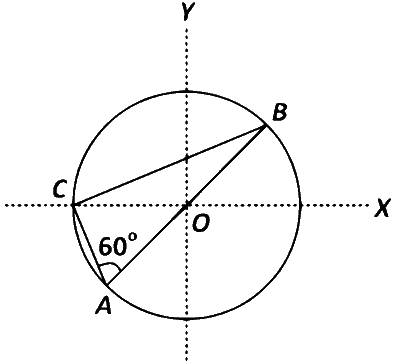
Consider a system of three charges $${q \over 3},{q \over 3}$$ and $$ - {{2q} \over 3}$$ placed at points A, B and C, respectively, as shown in the figure. Take O to be the centre of the circle of radius R and angle CAB = 60$$^\circ$$
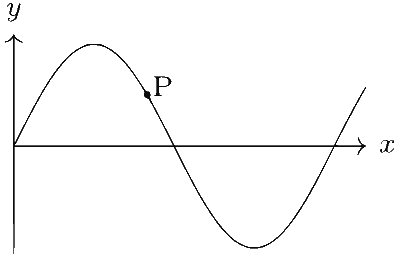
A transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10 cm/s. The wavelength of the waves is 0.5 m and its amplitude is 10 cm. At a particular time t, the snap-shot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is :
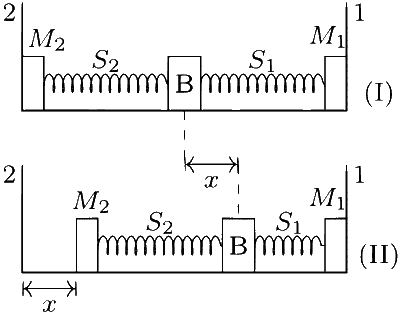
A block (B) is attached to two unstretched springs S1 and S2 with spring constants k and 4k respectively (see figure I). The other ends are attached to identical supports M1 and M2 not attached to the walls. The springs and supports have negligible mass. There is no friction anywhere. The block displaced towards wall 1 by a small distance x (figure II) and released. The block returns and moves a maximum distance y towards wall 2. Displacements x and y are measured with respect to the equilibrium position of the block B. The ratio $$\frac{y}{x}$$ is :
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
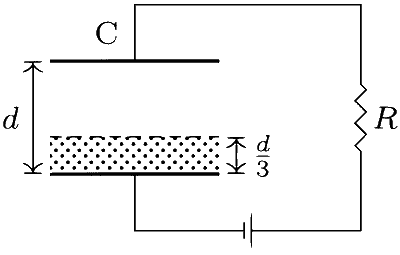
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K = 2. The level of liquid is $$\frac{d}{3}$$ initially. Suppose the liquid level decreases at a constant speed V, the time constant as a function of time t is:
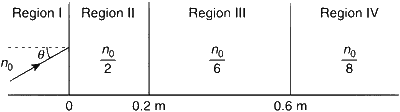
A light beam is travelling from Region I to Region IV (Refer figure). The refractive index in Regions I, II, III and IV are $${n_0},{{{n_0}} \over 2},{{{n_0}} \over 6}$$ and $${{{n_0}} \over 8}$$, respectively. The angle of incidence $$\theta$$ for which the beam just misses entering Region IV is
STATEMENT 1 : For practical purposes, the earth is used as a reference at zero potential in electrical circuits.
and
STATEMENT 2 : The electrical potential of a sphere of radius R with charge Q uniformly distributed on the surface is given by $${Q \over {4\pi {\varepsilon _0}R}}$$
STATEMENT 1 : The sensitivity of a moving coil galvanometer is increased by placing a suitable magnetic material as a core inside the coil.
and
STATEMENT 2 : Soft iron has a high magnetic permeability and cannot be easily magnetized or demagnetized.
Column I gives a list of possible set of parameters measured in some experiments. The variations of the parameters in the form of graphs are shown in Column II. Match the set of parameters given in Column I with the graphs given in Column II. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.
| Column I | Column II | ||
|---|---|---|---|
| (A) | Potential energy of a simple pendulum (y-axis) as a function of displacement (x) axis | (P) | 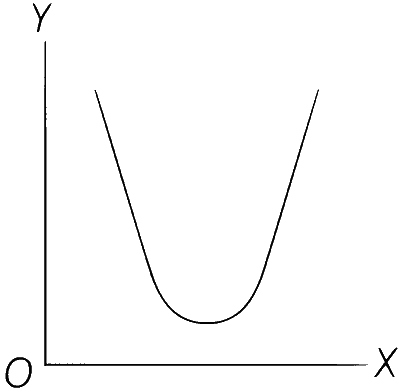 |
| (B) | Displacement (y-axis) as a function of time (x-axis) for a one dimensional motion at zero or constant acceleration when the body is moving along the positive x-direction | (Q) | 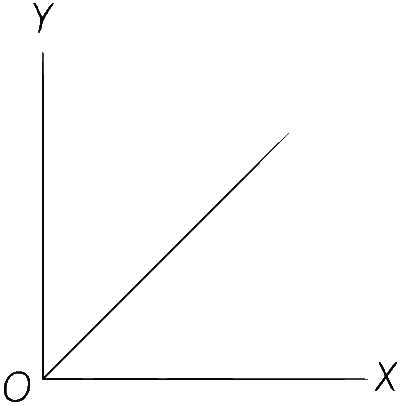 |
| (C) | Range of a projectile (y-axis) as a function of its velocity (x-axis) when projected at a fixed angle | (R) | 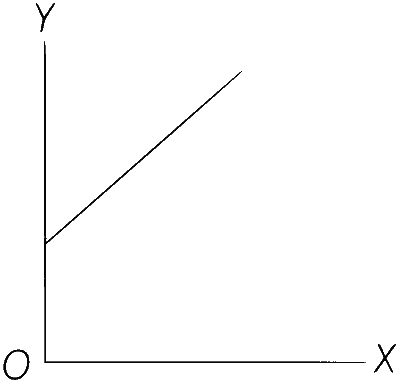 |
| (D) | The square of the time period (y-axis) of a simple pendulum as a function of its length (x-axis) | (S) | 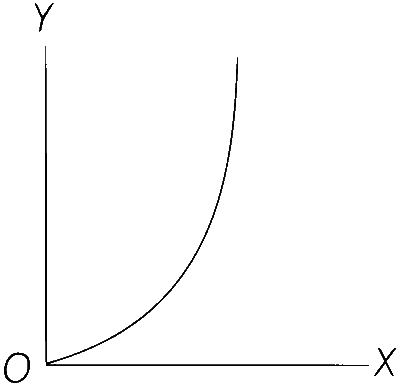 |
An optical component and an object S placed along its optic axis are given in Column I. The distance between the object and the component can be varied. The properties of images are given in Column II. Match all the properties of images from Column II with the appropriate components given in Column I. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.
| Column I | Column II | ||
|---|---|---|---|
| (A) | 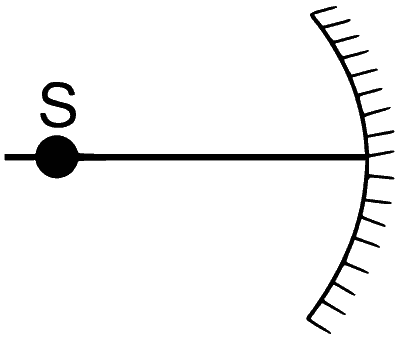 |
(P) | Real Image |
| (B) | 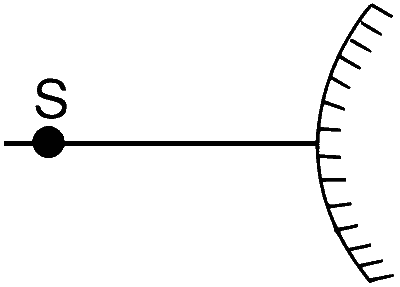 |
(Q) | Virtual Image |
| (C) | 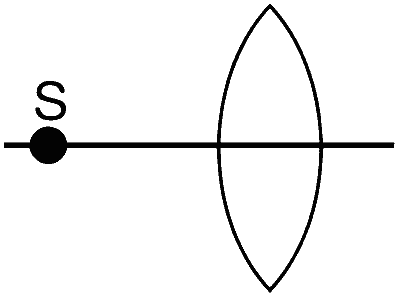 |
(R) | Magnified Image |
| (D) | 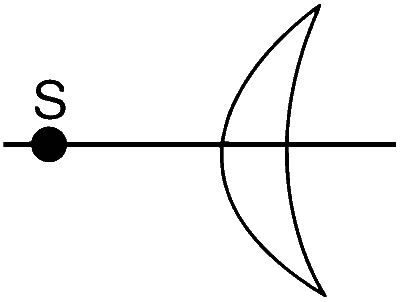 |
(S) | Image at infinity |
Column I contains a list of processes involving expansion of an ideal gas. Match this with Column II describing the thermodynamic change during this process. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.
| Column I | Column II | ||
|---|---|---|---|
| (A) | An insulated container has two chambers separated by a valve. Chamber I contains an ideal gas and the Chamber II has vacuum. The valve is opened.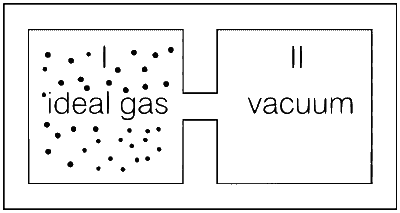 |
(P) | The temperature of the gas decreases |
| (B) | An ideal monatomic gas expands to twice its original volume such that its pressure P $$\propto$$ $$\frac{1}{\mathrm{V}^2}$$, where V is the volume of the gas | (Q) | The temperature of the gas increase or remains constant. |
| (C) | An ideal monoatomic gas expands to twice its original volume such that its pressure P $$\propto$$ $$\frac{1}{\mathrm{V}^{4/3}}$$, where V is its volume | (R) | The gas loses heat |
| (D) | An ideal monoatomic gas expands such that its pressure P and volume V follows the behaviour shown in the graph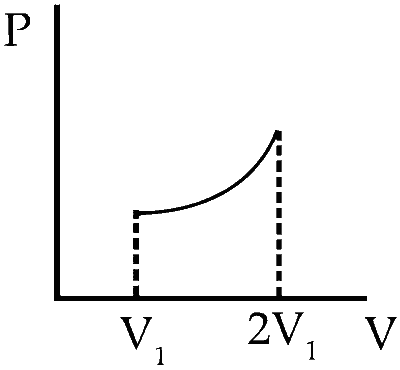 |
(S) | The gas gains heat |