JEE Advance - Physics (2008 - Paper 2 Offline - No. 7)
A glass tube of uniform internal radius (r) has a valve separating the two identical ends. Initially, the valve is in a tightly closed position. End 1 has a hemispherical soap bubble of radius r. End 2 has sub-hemispherical soap bubble as shown in figure. Just after opening the valve,
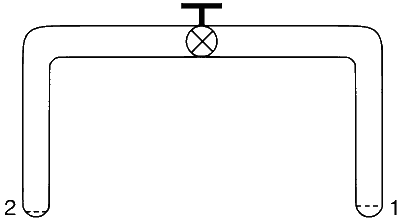
air from end 1 flows towards end 2. No change in the volume of the soap bubbles
air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases
no change occurs
air from end 2 flows towards end 1. Volume of the soap bubble at end 1 increases
Explanation
Given that,
$${r_2} > {r_1}$$
Just inside of soap bubble, the pressure
$${P_1} = {P_0} + {{4T} \over {{r_1}}}$$ ..... (i)
$${P_2} = {P_0} + {{4T} \over {{r_2}}}$$ .... (ii)
Hence, $${r_2} > {r_1}$$ then $${P_1} > {P_2}$$
Therefore, air from end 1 flows towards end 2. Volume of the soap bubble at end 1 decreases.
Comments (0)


