JEE Advance - Physics (2008 - Paper 2 Offline - No. 21)
An optical component and an object S placed along its optic axis are given in Column I. The distance between the object and the component can be varied. The properties of images are given in Column II. Match all the properties of images from Column II with the appropriate components given in Column I. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.
| Column I | Column II | ||
|---|---|---|---|
| (A) | 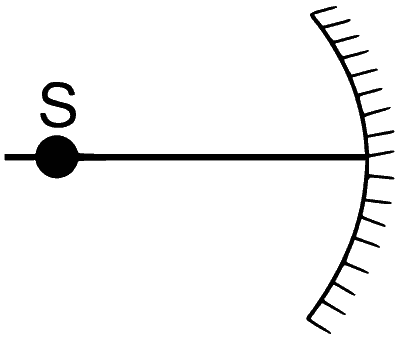 |
(P) | Real Image |
| (B) | 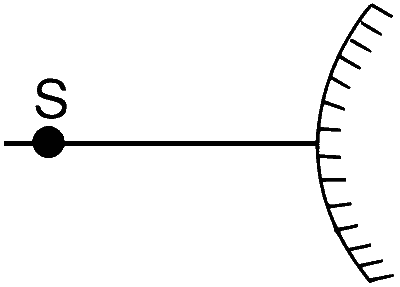 |
(Q) | Virtual Image |
| (C) | 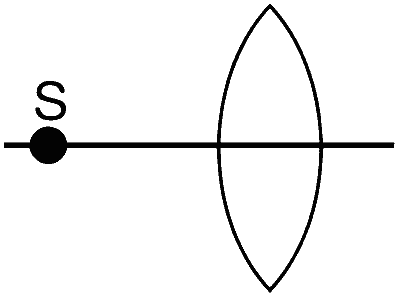 |
(R) | Magnified Image |
| (D) | 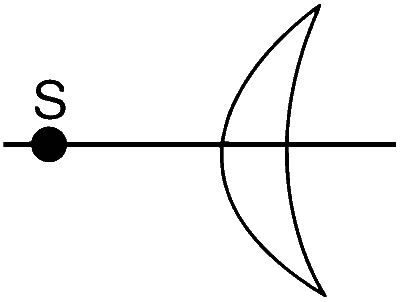 |
(S) | Image at infinity |
Explanation
(A) $$\to$$ P, Q, R, S
$$v = {f \over {1 - {f \over u}}},m = {{ - v} \over u}$$
For different values of u, we get different values of $$v$$(+ve, $$-$$ve or $$\infty$$). Like wise $$m$$ comes out to be positive, negative, greater than 1 etc.
(B) $$\to$$ Q
In case of a convex mirror we always get virtual, diminished image, between P and F.
(C) $$\to$$ P, Q, R, S
When object is at infinity, a real, inverted and diminished image is formed at F. When the object is brought closer to the lens. The image moves away from the lens and increase in size. (Image is between F and 2F). when the object is at 2F', the image is formed at 2F. The image is real, inverted and is of the same size. When the object is moved closer between 2F' and F', the image is real, inverted and magnified. When the object is at F' the image is real, inverted, highly magnified and is formed at infinity.
(D) $$\to$$ P, Q, R, S
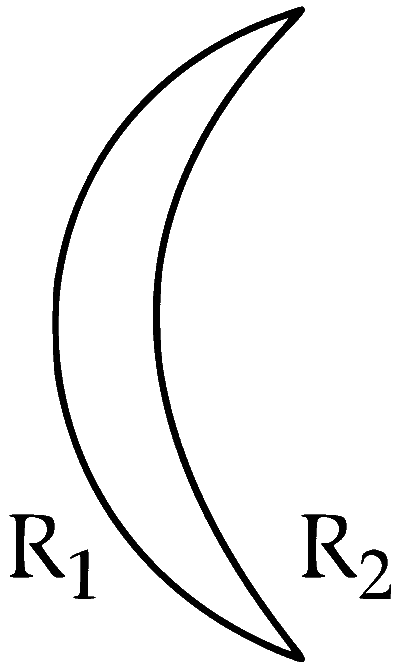
$${1 \over f} = (\mu - 1)\left[ {{1 \over {{R_1}}} - {1 \over {{R_2}}}} \right] = (\mu - 1)\left[ {{{{R_2} - {R_1}} \over {{R_1}{R_2}}}} \right]$$
Here $${R_1} < {R_2}$$
$$\therefore$$ $$f$$ is positive.
Therefore, it behaves like a convex lens.
Comments (0)


