JEE Advance - Physics (2008 - Paper 2 Offline - No. 20)
Column I gives a list of possible set of parameters measured in some experiments. The variations of the parameters in the form of graphs are shown in Column II. Match the set of parameters given in Column I with the graphs given in Column II. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.
| Column I | Column II | ||
|---|---|---|---|
| (A) | Potential energy of a simple pendulum (y-axis) as a function of displacement (x) axis | (P) | 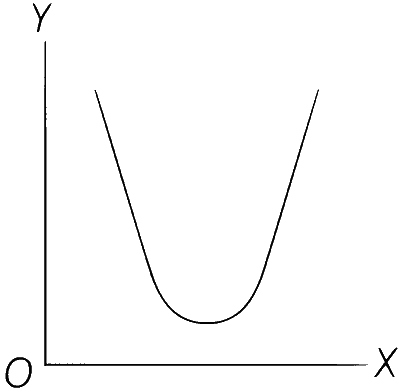 |
| (B) | Displacement (y-axis) as a function of time (x-axis) for a one dimensional motion at zero or constant acceleration when the body is moving along the positive x-direction | (Q) | 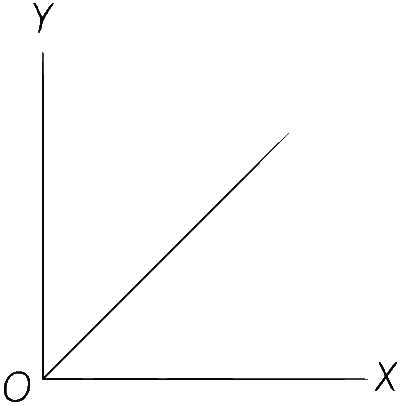 |
| (C) | Range of a projectile (y-axis) as a function of its velocity (x-axis) when projected at a fixed angle | (R) | 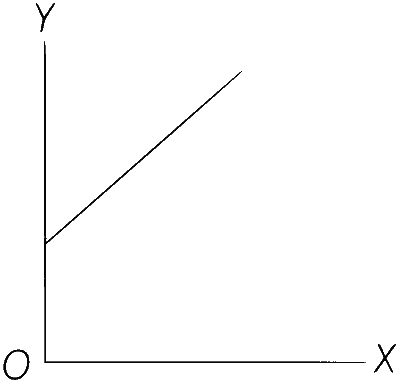 |
| (D) | The square of the time period (y-axis) of a simple pendulum as a function of its length (x-axis) | (S) | 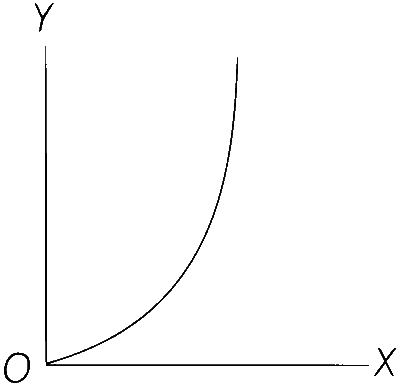 |
Explanation
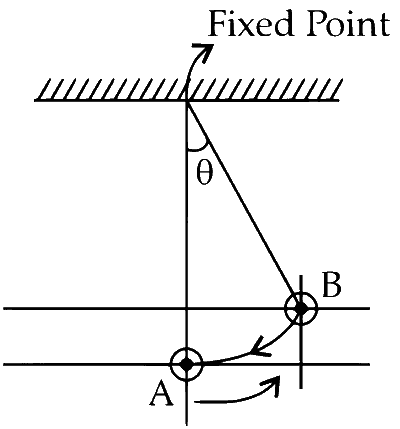
Potential energy at point A. U$$_\mathrm{A}$$ = 0,
Kinetic Energy K$$_\mathrm{A}$$ = maximum
Potential energy at point B, UB = maximum,
KB = 0
The graph of potential energy as function of displacement of a simple pendulum will be parabolic graph as given in option p. Hence (A) $$ \to $$ (P). The choice (S) is also correct if the mean position of the pendulum is at the origin. Hence (A) $$ \to $$ (P), (S).
(P) 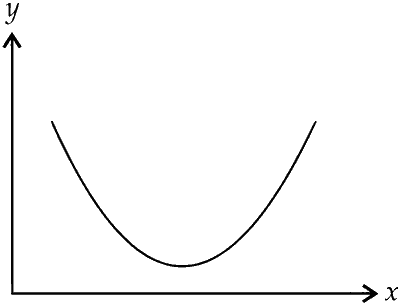
(S) 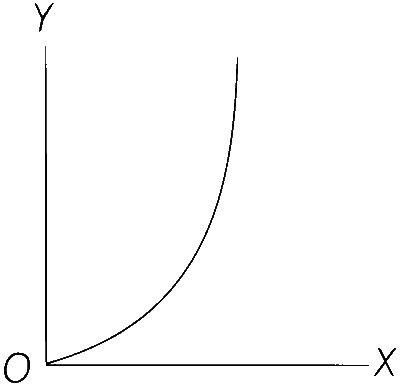
(B) 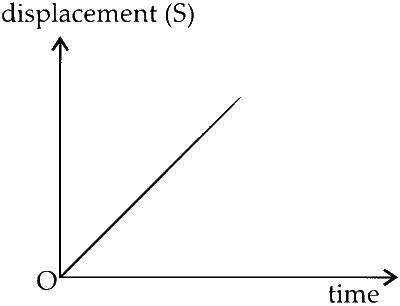
Slope of displacement time graph gives velocity.
$$\therefore$$ $$v = {{ds} \over {dt}}$$
If $$\overrightarrow a = 0$$ or constant
$$v = u + at$$
$$v = 0 + at$$
$$\therefore$$ $$a = v/t$$
$$a = $$ constant
(S) 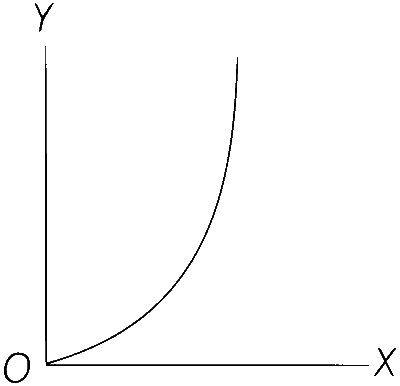
$$ \begin{aligned} & \text { (C) } \quad R=\frac{v^2 \sin 2 \theta}{g} \\ & \therefore \quad R \propto v^2 \rightarrow \operatorname{option}(\mathrm{S}) \end{aligned} $$
(D) $$T = 2\pi \sqrt {{l \over g}} $$
$$\therefore$$ $$T \propto \sqrt l $$
$${T^2} \propto l$$ is a straight line
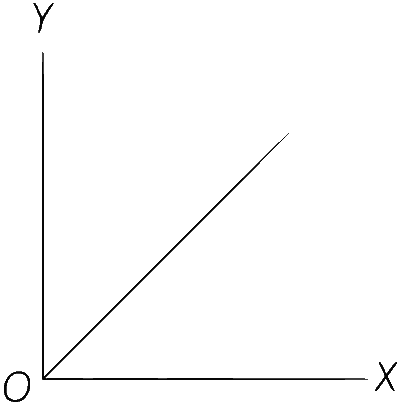
Comments (0)


