JEE Advance - Physics (2008 - Paper 2 Offline - No. 2)
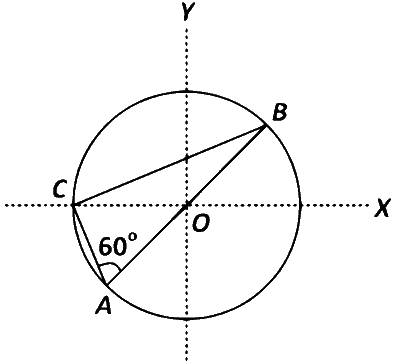
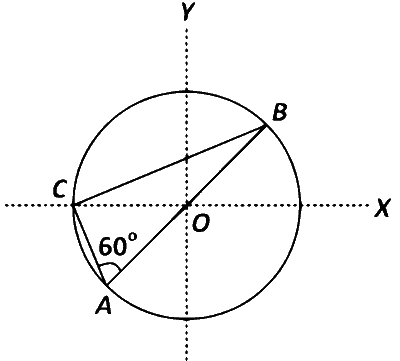
Consider a system of three charges $${q \over 3},{q \over 3}$$ and $$ - {{2q} \over 3}$$ placed at points A, B and C, respectively, as shown in the figure. Take O to be the centre of the circle of radius R and angle CAB = 60$$^\circ$$
Explanation
Electric field at point O is vector sum of electric field due to all three point charges individually.
$$\overrightarrow E = \overrightarrow {{E_A}} + \overrightarrow {{E_B}} + \overrightarrow {{E_C}} $$ and $$\overrightarrow {{E_A}} = - \overrightarrow {{E_B}} $$
So, $$\overrightarrow E = \overrightarrow {{E_C}} = {{2q/3} \over {4\pi {\varepsilon _0}.{R^2}}}$$ along $$\overrightarrow {OC} $$
$$ = {q \over {6\pi \varepsilon _0^2.{R^2}}}$$ along $$\overrightarrow {OC} $$
$$ = {{ + q'} \over {6\pi \varepsilon _0^2.{R^2}}}\widehat i$$
$$ = {{ - q'} \over {6\pi \varepsilon _0.{R^2}}}\widehat j$$
From geometry, we can find that $$\angle$$ABC = 30$$^\circ$$ and $$\angle$$ACB = 90$$^\circ$$
So, AB = 2R, AC = R, BC = $$\sqrt3$$R
Total potential energy of the system is,
$$U = {1 \over {4\pi {\varepsilon _0}}}\left[ {{{q/3 \times q/3} \over {2R}} - {{q/3 \times 2q/3} \over R} - {{q/3 \times 2q/3} \over {\sqrt 3 R}}} \right] \ne 0$$
$$F = {{q/3 \times q/3} \over {4\pi {\varepsilon _0} \times {{(\sqrt 3 R)}^2}}} = {{{q^2}} \over {54\pi {\varepsilon _0}{R^2}}}$$
Potential at point O is,
$$V = {{q/3 \times q/3 - 2q/3} \over {4\pi {\varepsilon _0}R}} = 0$$
Comments (0)


