JEE Advance - Physics (2008 - Paper 2 Offline - No. 9)
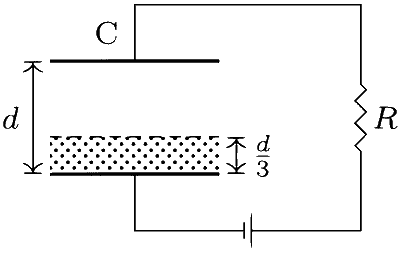
A parallel plate capacitor C with plates of unit area and separation d is filled with a liquid of dielectric constant K = 2. The level of liquid is $$\frac{d}{3}$$ initially. Suppose the liquid level decreases at a constant speed V, the time constant as a function of time t is:
Explanation
Time constant ($$\tau$$) = RC$$_{eq}$$
Where R = Resistance
C$$_{eq}$$ = equivalent capacitance
And, $$v = {{ - dx} \over {dt}} \Rightarrow dx = - vdt$$
$$ \Rightarrow \int_{d/3}^x {dx = - v\int_0^t {dt} } $$
$$ \Rightarrow [x]_{d/3}^x = - v[t]_0^t$$
$$x - {d \over 3} = - vt$$
$$x = {d \over 3} - vt$$ ..... (i)
And also, $${1 \over {{C_{eq}}}} = {1 \over {{C_1}}} + {1 \over {{C_2}}} = {1 \over {{{{\varepsilon _0}A} \over {(d - x)}}}} + {1 \over {{{{\varepsilon _0}Ak} \over x}}}$$
$${1 \over {{C_{eq}}}} = {{d - x} \over {{\varepsilon _0}A}} + {x \over {{\varepsilon _0}Ak}}$$
$$ = {1 \over {{\varepsilon _0}A}}\left[ {d - x + {x \over k}} \right]$$
$$ = {1 \over {{\varepsilon _0}A}}\left[ {{{(d - x)k + x} \over k}} \right]$$
$${1 \over {{C_{eq}}}} = {1 \over {{\varepsilon _0}Ak}}[dk - xk + x]$$
$$\therefore$$ $${C_{eq}} = {{{\varepsilon _0}A} \over {kd + x(1 - k)}}$$ .... (ii)
Given, $$A = 1,k = 2,x = {d \over 3} - vt$$
Hence, $${C_{eq}} = {{{\varepsilon _0} \times 1} \over {2d + \left[ {{d \over 3} - vt} \right](1 - 2)}}$$
$$ = {{6{\varepsilon _0}} \over {5d + 3vt}}$$
Therefore, $$\tau = R{C_{eq}} = {{6R{\varepsilon _0}} \over {5d + 3vt}}$$
Comments (0)


