Sign In

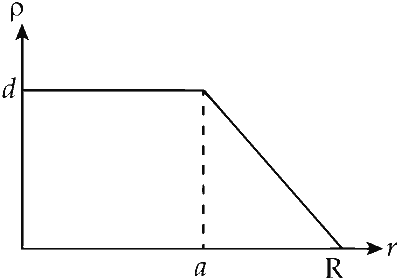
JEE Advance - Physics (2008 - Paper 2 Offline - No. 15)

The nuclear charge (Ze) is non-uniformly distributed within a nucleus of radius R. The charge density $$\rho(r)$$ [charge per unit volume] is dependent only on the radical distance r from the centre of the nucleus as shown in figure. The electric field is only along the radial direction.

The nuclear charge (Ze) is non-uniformly distributed within a nucleus of radius R. The charge density $$\rho(r)$$ [charge per unit volume] is dependent only on the radical distance r from the centre of the nucleus as shown in figure. The electric field is only along the radial direction.

The nuclear charge (Ze) is non-uniformly distributed within a nucleus of radius R. The charge density $$\rho(r)$$ [charge per unit volume] is dependent only on the radical distance r from the centre of the nucleus as shown in figure. The electric field is only along the radial direction.

For a = 0, the value of d (maximum value of $$\rho$$ as shown in the figure) is
$${{3Ze} \over {4\pi {R^3}}}$$
$${{3Ze} \over {\pi {R^3}}}$$
$${{4Ze} \over {3\pi {R^3}}}$$
$${{Ze} \over {3\pi {R^3}}}$$

Explanation

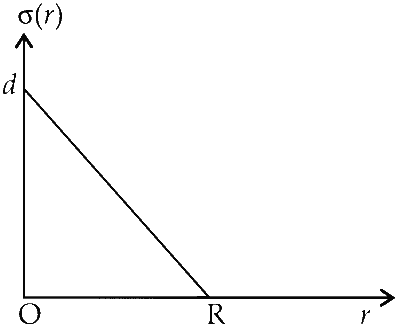
For a = 0, the graph is as shown, the equation for the graph line is

IIT-JEE 2008 Paper 2 Offline Physics - Electrostatics Question 9 English Explanation 1

The charge in the dotted element shown in figure is

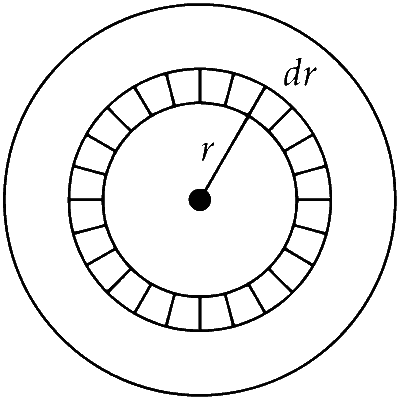
IIT-JEE 2008 Paper 2 Offline Physics - Electrostatics Question 9 English Explanation 2

$$dq = \sigma \times 4\pi {r^2}dr$$

$$\therefore$$ $$dq = \left( {d - {d \over R}r} \right)4\pi {r^2}dr$$

$$ \Rightarrow Ze = \int_0^R {4\pi d{r^2}dr - \int_0^R {{{4\pi d} \over R}{r^3}dr} } $$

$$Ze = 4\pi d{{{R^3}} \over 3} - {{4\pi d} \over R}{{{R^4}} \over 4}$$

$$\therefore$$ $${{Ze} \over {4\pi d{R^3}}} = {1 \over 3} - {1 \over 4} = {1 \over {12}}$$

$$\therefore$$ $$d = {{3Ze} \over {\pi {R^3}}}$$

Comments (0)

Advertisement