JEE Advance - Physics (2008 - Paper 2 Offline - No. 6)
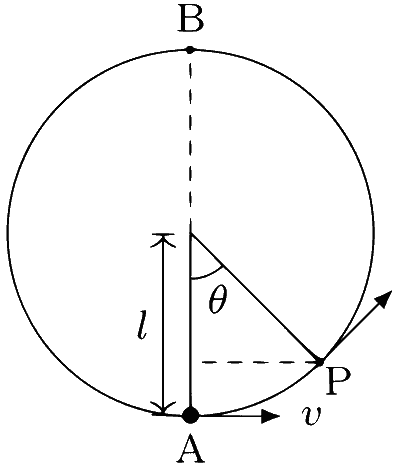
A bob of mass M is suspended by a massless string of length L. The horizontal velocity V at position A is just sufficient to make it reach the point B. The angle $$\theta$$ at which the speed of the bob is half of that at A, satisfies,
Explanation
The bob of mass m requires velocity to reach at a point with vertical circular motion.
$$V = \sqrt {5gl} $$
Then, $$h = L - L\cos \theta = L(1 - \cos \theta )$$
Applying law of conservation of energy at point A & C
Kinetic energy (K.E)A + Potential energy (UA) = Kinetic energy (K.EC) + Potential energy (UC)
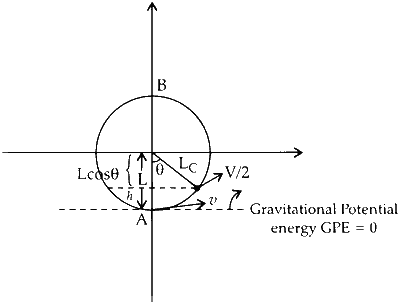
$$ \Rightarrow {1 \over 2}m{V^2} + 0 = {1 \over 2}m{\left( {{{\sqrt {5gl} } \over 2}} \right)^2} + mgL(1 - \theta )$$
$$ \Rightarrow {{5L} \over 2} = {{5L} \over 8} + L(1 - \cos \theta )$$ ($$\because$$ $$V = \sqrt {5gl} $$)
$$ \Rightarrow {5 \over 2} - {5 \over 8} = 1 - \cos \theta $$
$$ \Rightarrow {{20 - 5} \over 8} = 1 - \cos \theta $$
$$ \Rightarrow \cos \theta = 1 - {{15} \over 8}$$
$$ \Rightarrow \cos \theta = {{ - 7} \over 8}$$
$$ \Rightarrow \theta = 152^\circ $$
$$\therefore$$ $${{3\pi } \over 4} < \theta < \pi $$
Comments (0)


