JEE Advance - Physics (2008 - Paper 2 Offline - No. 10)
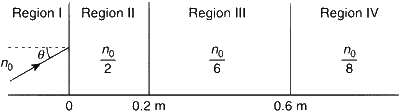
A light beam is travelling from Region I to Region IV (Refer figure). The refractive index in Regions I, II, III and IV are $${n_0},{{{n_0}} \over 2},{{{n_0}} \over 6}$$ and $${{{n_0}} \over 8}$$, respectively. The angle of incidence $$\theta$$ for which the beam just misses entering Region IV is
Explanation
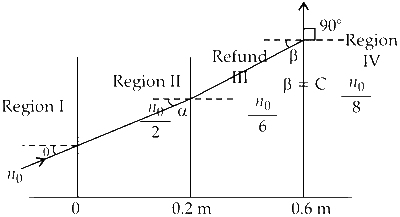
From Snell's laws
$${\mu _1}\sin \theta = {\mu _2}\sin {\theta _2}$$
Case I : Region I
$${n_0}\sin \theta = {{{n_0}} \over 2}\sin \alpha $$ ...... (i)
Case II : Region II
$${{{n_0}} \over 2}\sin \alpha = {{{n_0}} \over 6}\sin {\theta _c}$$ ..... (ii) ($$\therefore$$ $$\beta = {\theta _c}$$)
Case II : Region III
$${{{n_0}} \over 6}\sin {\theta _c} = {{{n_0}} \over 8}\sin 90^\circ $$
$$ \Rightarrow {{{n_0}} \over 6}\sin {\theta _c} = {{{n_0}} \over 8}$$ ..... (iii)
From equation (i), (ii) and (iii), we have,
$${n_0}\sin \theta = {{{n_0}} \over 8}$$
$$ \Rightarrow \sin \theta = {1 \over 8}$$
$$ \Rightarrow \theta = {\sin ^{ - 1}}\left( {{1 \over 8}} \right)$$
Comments (0)


