JEE Advance - Physics (2008 - Paper 2 Offline - No. 4)
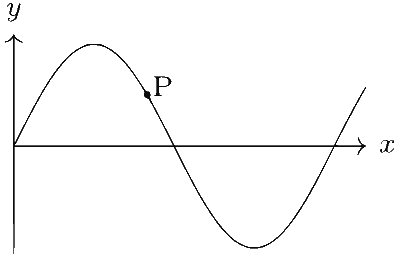
A transverse sinusoidal wave moves along a string in the positive x-direction at a speed of 10 cm/s. The wavelength of the waves is 0.5 m and its amplitude is 10 cm. At a particular time t, the snap-shot of the wave is shown in figure. The velocity of point P when its displacement is 5 cm is :
Explanation
Velocity of point $$p=dy/dt$$
= $$-$$(velocity of wave $$\times$$ $$dy/dx$$)
Here, $$dy/dx=$$ negative ($$-$$ve). Therefore, velocity at point P is positive and is along X-axis only.
Equation of a wave moving in positive X-axis is given as,
$$y = A\sin (wt - \phi )$$ .... (i)
or, $${V_P} = Aw\cos (wt - \phi )$$ .... (ii)
Here, $$y' = 5$$ cm, $$A = 10$$ cm
$$\therefore$$ $$5 = 10\sin (wt - \phi ) \Rightarrow wt - \phi = 30^\circ $$ .... (iii)
Put equation (iii) in equation (ii),
$${V_P} = 0.10 \times w\cos 30^\circ $$
Now, $$V = {V_\lambda }$$, $$\therefore$$ $$v = V/\lambda = {{0.10} \over {0.5}} = 0.2$$
$$\therefore$$ $$w = 2\pi v = 2\pi \times 0.2 = 0.4\pi $$
$$ \Rightarrow {V_P} = 0.1 \times 0.4\pi \times {{\sqrt 3 } \over 2} = {{\sqrt 3 } \over {50}}\pi \,\widehat j$$ m/s
It is in positive Y-direction.
Comments (0)


