JEE Advance - Physics (2008 - Paper 2 Offline - No. 22)

Column I contains a list of processes involving expansion of an ideal gas. Match this with Column II describing the thermodynamic change during this process. Indicate your answer by darkening the appropriate bubbles of the 4 $$\times$$ 4 matrix given in the ORS.

	Column I		Column II
(A)	An insulated container has two chambers separated by a valve. Chamber I contains an ideal gas and the Chamber II has vacuum. The valve is opened.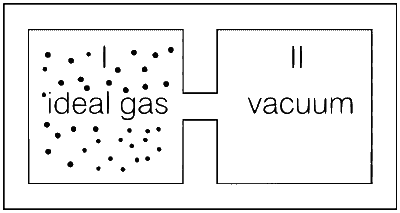	(P)	The temperature of the gas decreases
(B)	An ideal monatomic gas expands to twice its original volume such that its pressure P $$\propto$$ $$\frac{1}{\mathrm{V}^2}$$, where V is the volume of the gas	(Q)	The temperature of the gas increase or remains constant.
(C)	An ideal monoatomic gas expands to twice its original volume such that its pressure P $$\propto$$ $$\frac{1}{\mathrm{V}^{4/3}}$$, where V is its volume	(R)	The gas loses heat
(D)	An ideal monoatomic gas expands such that its pressure P and volume V follows the behaviour shown in the graph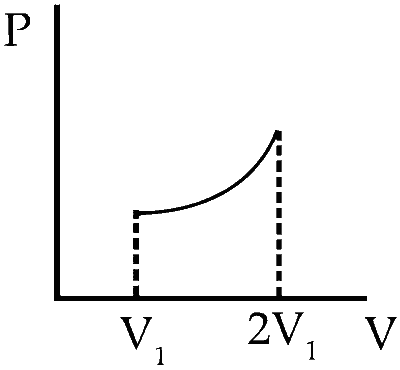	(S)	The gas gains heat

A $$\to$$ (P); B $$\to$$ (P, Q); C $$\to$$ (R, S); D $$\to$$ (P, R)

A $$\to$$ (P); B $$\to$$ (R, S); C $$\to$$ (P, Q); D $$\to$$ (Q, S)

A $$\to$$ (Q); B $$\to$$ (R, S); C $$\to$$ (P, S); D $$\to$$ (P, R)

A $$\to$$ (Q); B $$\to$$ (P, Q); C $$\to$$ (P, S); D $$\to$$ (Q, S)

Explanation

As the ideal gas expands in vacuum, no work is done i.e., w = 0

Container is insulated, so no heat lost or gained i.e., Q = 0.

According to the first law of thermodynamics

$$\Delta$$U = Q + w

$$\therefore$$ $$\Delta$$U = 0

Therefore, no change in the temperature of the gas.

(b) $$\to$$ ($$p, r$$) :

Given, PV$$^2$$ = constant ... (i)

For ideal gas, $${{PV} \over T}$$ = constant .... (ii)

From (i) and (ii) V $$\mu$$ T = constant

As gas expands, its volume increase and temperature decreases.

$$\therefore$$ (p) is the correct.

Also, Q = nC$$\Delta$$T .... (i)

Where C = molar specific heat

For a polytropic process,

$$C = {C_V} + {R \over {1 - n}}$$ and

PV$$^n$$ = constant

Here, PV$$^2$$ = constant, where n = 2

$$\therefore$$ $$C = {C_V} + {R \over {1.2}} = {C_V} - R$$

For monoatomic gas,

$${C_V} = {3 \over 2}R$$

$$\therefore$$ $$C = {3 \over 2}R - R = {R \over 2}$$

Substituting this value in (1), we get

$$Q = n \times {R \over 2} \times \Delta T$$

Temperature decreases i.e., $$\Delta$$T is negative. Therefore, Q is negative. This is turn mean that heat is lost by the gas during the process.

So (r) is the correct option.

V$$^{1/3}$$ $$\times$$ T = constant

$$\Rightarrow$$ As the gas expands and volume increases, the temperature decreases. Therefore (P) is the correct option.

In the process, $$x = {4 \over 3}$$

$$\therefore$$ $$C = {C_V} + {R \over {1 - {4 \over 3}}} = {3 \over 2}R + {{3R} \over { - 1}}$$

$$ = {3 \over 2}R - 3R = - {{3R} \over 2}$$

$$\therefore$$ $$Q = n\left( { - {3 \over 2}R} \right)\Delta t$$

As $$\Delta t$$ = $$-$$negative ($$-$$ve), Q = positive (+ve). That means heat is gained by the gas during the process.

(s) is correct.

(d) $$\to$$ (q, s)

$$\Delta T = {{\Delta (PV)} \over {nR}}$$

$$\Delta (PV)$$ = Positive $$\therefore$$ $$\Delta$$T = positive

$$\therefore$$ Temperature increase (Q) is the correct option.

From graph it is clear that, during the process the pressure of the gas increases which shows that the internal energy of the gas has increased. Also, the volume increases which means work is done by the system which needs energy. We conclude from the above fact that gas gains heat during the process.

(S) is correct.

JEE Advance - Physics (2008 - Paper 2 Offline - No. 22)

Explanation

Comments (0)