JEE Advance - Physics (2008 - Paper 2 Offline - No. 5)
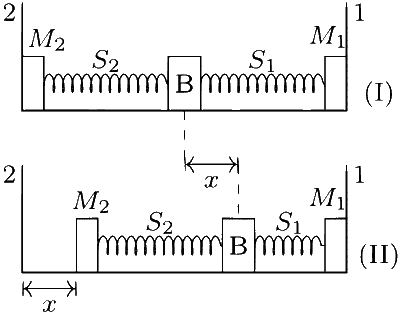
A block (B) is attached to two unstretched springs S1 and S2 with spring constants k and 4k respectively (see figure I). The other ends are attached to identical supports M1 and M2 not attached to the walls. The springs and supports have negligible mass. There is no friction anywhere. The block displaced towards wall 1 by a small distance x (figure II) and released. The block returns and moves a maximum distance y towards wall 2. Displacements x and y are measured with respect to the equilibrium position of the block B. The ratio $$\frac{y}{x}$$ is :
Explanation
When the block B is displaced towards wall-1 only spring S$$_1$$ is compressed and S$$_2$$ is in natural state.
If spring S$$_2$$ is not attached to wall but it is free but it gain momentum ($$\uparrow$$) and moves towards S$$_1$$.
The spring S$$_1$$ comes to natural length and spring S$$_2$$ gets compressed.
So if there is no frictional force i.e.,
$$fr=0$$
So potential energy of spring S$$_1$$ as the potential energy of spring.
Hence, $${(PE)_{{S_1}}} = {(PE)_{{S_2}}}$$
$$ \Rightarrow {1 \over 2}{k_1}{x^2} = {1 \over 2}{k_2}y$$
$$ \Rightarrow 1k{x^2} = (4k){y^2} \Rightarrow {x^2} = 4{y^2}$$
Potential energy of spring.
Hence, $${(PE)_{{S_1}}} = {(PE)_{{S_2}}}$$
$$ \Rightarrow {1 \over 2}{k_1}{x^2} = {1 \over 2}{k_2}{y^2}$$
$$ \Rightarrow {1 \over 2}k{x^2} = {1 \over 2}(4k){y^2}$$
$$ \Rightarrow {x^2} = 4{y^2}$$
$$ \Rightarrow {y \over x} = {1 \over 2}$$
Comments (0)


