Sign In

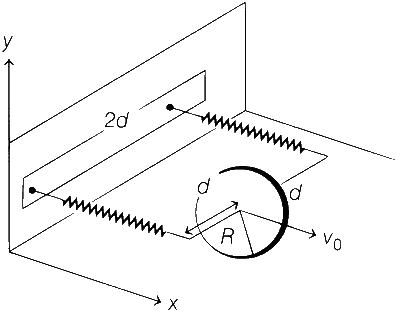
JEE Advance - Physics (2008 - Paper 2 Offline - No. 17)

A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant $$k$$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in a horizontal plane. The unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity $${\overrightarrow V _0} = {V_0}\widehat i$$. the coefficient of friction is $$\mu$$.

A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant $$k$$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in a horizontal plane. The unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity $${\overrightarrow V _0} = {V_0}\widehat i$$. the coefficient of friction is $$\mu$$.

A uniform thin cylindrical disk of mass M and radius R is attached to two identical massless springs of spring constant $$k$$ which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in a horizontal plane. The unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity $${\overrightarrow V _0} = {V_0}\widehat i$$. the coefficient of friction is $$\mu$$.

The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is :
$$ - kx$$
$$ - 2kx$$
$$ - {{2kx} \over 3}$$
$$ - {{4kx} \over 3}$$

Explanation

When the disc is at a distance x from the mean position (equilibrium position), the force acting on the disc are give below.

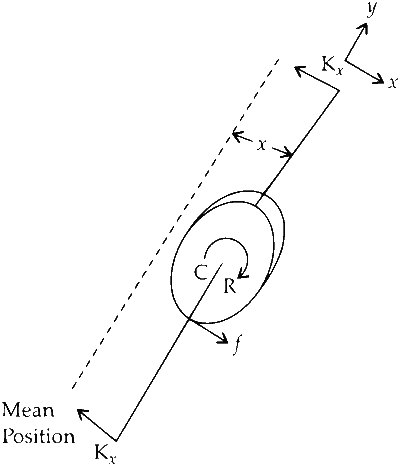
IIT-JEE 2008 Paper 2 Offline Physics - Rotational Motion Question 13 English Explanation

$$\therefore -2kx+f=-M_{ac}$$ ..... (i)

Where $$a_c$$ = acceleration of centre of mass.

The torque acting on the disc about its centre of mass C is

$$\tau = f \times R = I \times {a_c}$$

$$\therefore$$ $$f = {{I\alpha } \over R} = {{{1 \over 2}M{R^2}} \over R} \times {{{a_c}} \over R}$$

[$$\therefore$$ $$I = {1 \over 2}M{R^2},{a_c} = R{a_c}$$ for rolling without slipping]

$$\therefore$$ $$f = {1 \over 2}M{a_c}$$ ...... (ii)

From eq. (i) and (ii),

$$ - 2kx + {1 \over 2}M{a_c} = - M{a_c}$$

$$ \Rightarrow {3 \over 2}M{a_c} = 2kx$$

$$ \Rightarrow M{a_c} = {{4kx} \over 3}$$

$$\Rightarrow$$ Net external force acting on the disc when its centre of mass is at displacement x with respect to the equilibrium position $$ = {{ - 4kx} \over 3}$$ directed towards the equilibrium.

Comments (0)

Advertisement