एक रेडियोधर्मी नमूने में, $${}_{19}^{40}K$$ नाभिक स्थिर $${}_{20}^{40}Ca$$ नाभिक में 4.5 $$ \times $$ 10^-10 प्रति वर्ष क्षय स्थिरांक के साथ या स्थिर $${}_{18}^{40}Ar$$ नाभिक में 0.5 $$ \times $$ 10^-10 प्रति वर्ष क्षय स्थिरांक के साथ क्षय करता है। दिए गए कि इस नमूने में सभी स्थिर $${}_{20}^{40}Ca$$ और $${}_{18}^{40}Ar$$ नाभिक केवल $${}_{19}^{40}K$$ नाभिक द्वारा उत्पन्न होते हैं। $t$$ \times $$ 10⁹ वर्षों में, यदि स्थिर $${}_{20}^{40}Ca$$ और $${}_{18}^{40}Ar$$ नाभिक के योग का रेडियोधर्मी $${}_{19}^{40}K$$ नाभिक के साथ अनुपात 99 है, तो t का मान होगा

[दिया गया: In 10 = 2.3]

एक धारा वाहक तार एक धातु की छड़ को गरम करता है। तार छड़ को एक स्थिर शक्ति (P) (constant power) प्रदान करता है | यह धातु छड़ एक अचालक बर्तन में रखी गयी है | यह पाया गया कि धातु का तापमान $$(T)$$ समय $$(t)$$ के साथ निम्न ढंग से परिवर्तित होता है

$$T(t)=T_{0}\left(1+\beta t^{\frac{1}{4}}\right)$$

जहां $$\beta$$ एक उपयुक्त विमा का स्थिरांक है जबकि $$T_{0}$$ तापमान का है । धातु की ऊष्मा धारिता है,

$$R$$ त्रिज्या के एक पतले गोलीय अचालक कोश (spherical insulating shell) पर आवेश एकसमान रूप से इस तरह से वितरित है कि इसकी सतह पर विभव $$V_{0}$$ है। इसमें एक छोटे क्षेत्रफल $$\alpha 4 \pi R^{2}$$ $$(\alpha \ll 1)$$ वाला एक छिद्र बाकी कोश को प्रभावित किए बिना बनाया जाता है। निम्नलिखित कथनों में से कौन सा सही है ?

मान लीजिये मुक्त आकाश (free space) में एक गोलाकार गैस के बादल का द्रव्यमान घनत्व $$\rho(r)$$ है तथा इसकी केन्द्र से त्रिज्य (radial) दूरी $$r$$ है | यह गैसीय बादल $$m$$ द्रव्यमान के समान कणों से बना है जो कि एक समकेंद्रीय वृत्ताकार कक्षाओं में समान गतिज ऊर्जा $$K$$ से घूम रहे हैं। इन कणों पर पारस्परिक गुरुत्वाकर्षण बल लग रहा है। यदि $$\rho(r)$$ समय के साथ एक स्थिर राशि है, तब कणों का संख्या घनत्व $$n(r)=\rho(r) / m$$ का मान होगा,

[ $$G$$ सार्वत्रिक गुरुत्वीय नियतांक है]

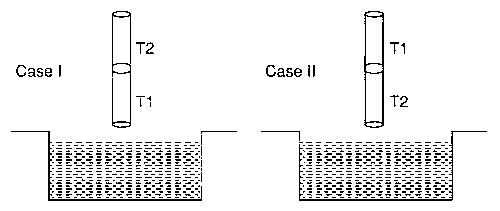
दो भित्न पदार्थो की एक समान $$0.2 \mathrm{~mm}$$ त्रिज्या वाली दो केशनलियों $$\mathrm{T} 1$$ तथा $$\mathrm{T} 2$$, जिनके पानी के साथ संपर्क कोण (contact angle) क्रमशः $$0^{\circ}$$ तथा $$60^{\circ}$$ हैं, को जोड़कर एक केशनली बनाते हैं । इस केशनली को चित्रानुसार दो भिन्न विन्यास-। और विन्यास-II में पानी में ऊर्ध्वाधर डुबाया जाता है। निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

[पानी का पृष्ठतनाव (surface tension) $$=0.075 \mathrm{~N} / \mathrm{m}$$, पानी का घनत्व $$=1000 \mathrm{~kg} / \mathrm{m}^{3}$$ तथा $$\left.g=10 \mathrm{~m} / \mathrm{s}^{2}\right]$$

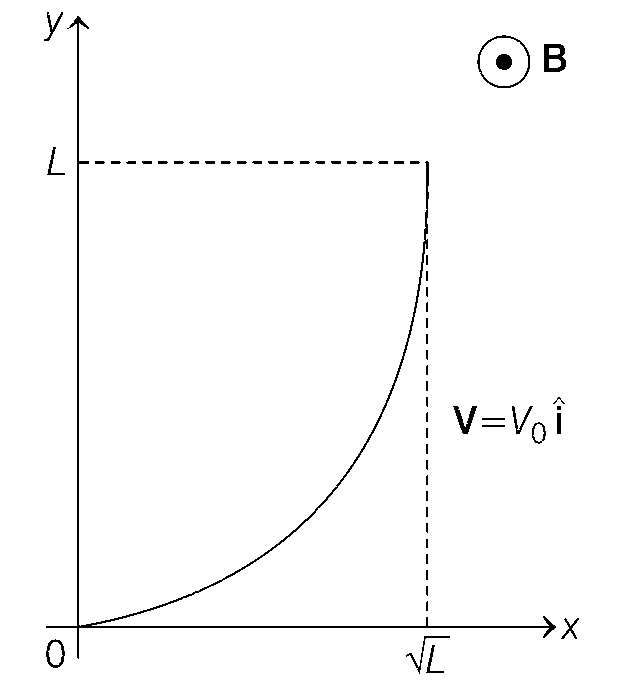
चित्रानुसार एक असमान चुंबकीय क्षेत्र $$\vec{B}=B_{0}\left(1+\left(\frac{y}{L}\right)^{\beta}\right) \hat{k}$$ में एक परवलयाकार (parabolic shape), आरंभ में $$y=x^{2}$$ वाला, विद्युत चालक तार वेग $$\vec{V}=V_{0} \hat{\imath}$$ से चल रहा है । यदि $$V_{0}, B_{0}, L$$ तथा $$\beta$$ धनात्मक नियतांक हैं एवं तार के सिरों के मध्य उत्पत्र विभवांतर $$\Delta \phi$$ है, तब निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

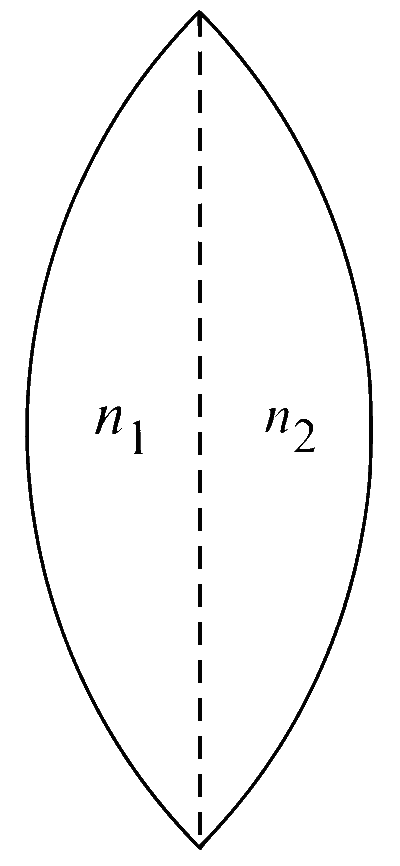
चित्र में दर्शाया गया एक पतला उत्तल लेंस दो पदार्थों से मिलकर बना है, जिनके अपवर्तनांक (refractive index) क्रमशः $$n_{1}$$ और $$n_{2}$$ हैं। लेंस के बाएँ और दाएँ पृष्ठों की वक्रता त्रिज्याएँ समान हैं। $$n_{1}=n_{2}=n$$ के लिए लेंस की फोकस दूरी $$f$$ है। जब $$n_{1}=n$$ और $$n_{2}=n+\Delta n$$ है, तब फोकस दूरी $$f+\Delta f$$ है । यह मानते हुए कि $$\Delta n \ll(n-1)$$ और $$1 < n < 2$$, निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

एकपरमाणुक आदर्श गैस का एक मोल एक ऊष्मागतिकीय चक्र (thermodynamic cycle) से गुजरता है, जिसे आयतन-तापमान $$(\mathrm{V}-\mathrm{T})$$ ग्राफ़ चित्र में दिखाया गया है। निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

[$$R$$ गैस नियतांक है ]

प्रदर्शित परिपथ में, आरम्भ में संधारित्रों पर कोई आवेश नहीं है और कुंजी $$\mathrm{S}_{1}$$ और $$\mathrm{S}_{2}$$ खुली हैं। संधारित्रों के मान $$C_{1}=10 ~\mu \mathrm{F}, C_{2}=30 \mu \mathrm{F}$$ और $$C_{3}=C_{4}=80 ~\mu \mathrm{F}$$ हैं। निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

एक $$R$$ त्रिज्या वाले आवेशित कोश पर कुल आवेश $$Q$$ है। एक लंबाई $$h$$ और त्रिज्या $$r$$ वाले बेलनाकार बंद पृष्ठ, जिसका केंद्र कोश के केंद्र पर ही है, से गुजरने वाला वैद्युत फ्लक्स (flux) $$\Phi$$ है | यहाँ बेलन का केंद्र इसके अक्ष पर एक बिन्दु है जो कि ऊपरी और निचली सतह से समान दूरी पर है। निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

[ मुक्त आकाश (free space) की वैद्युतशीलता $$\epsilon_{0}$$ है ]

दो एकसमान चलकुंडली धारामापी (galvanometer) जिनके प्रतिरोध $$10 \Omega$$ हैं तथा इनमें $$2 ~\mu \mathrm{A}$$ पर पूर्णस्केल विक्षेप (full-scale deflection) मिलता है । इनमें से एक को $$100 ~\mathrm{mV}$$ पूर्णस्केल मापन योग्य वोल्टमीटर तथा दूसरे को $$1 \mathrm{~mA}$$ पूर्णस्केल मापन योग्य अमीटर में उपयुक्त प्रतिरोधों का प्रयोग करते हुए परिवर्तित करते हैं। ओम का नियम (Ohm's law) प्रयोग में $$R=1000 \Omega$$ प्रतिरोध एवं एक आदर्श सेल के साथ इन दोनों का उपयोग विभव और धारा को मापने के लिये किया जाता है। निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?

मान लें कि एक ऐसी प्रणाली है जिसमें द्रव्यमान और कोणीय संवेग विमाहीन हैं। यदि लंबाई का आयाम L है, तो निम्नलिखित में से कौन सा कथन सही है?

एक $$C$$ धारिता वाले समान्तर प्लेट संधारित्र के प्लेटों के बीच की दूरी $$d$$ है और प्रत्येक प्लेट का क्षेत्रफल $$A$$ है | प्लेटों के बीच, पूरे स्थान को प्लेटों के समान्तर, $$\delta=\frac{d}{N}$$ मोटाई वाली $$N$$ परावैद्युत परतों से भर देते हैं। $$m^{\text {th }}$$ परत का परावैद्युतांक $$K_{m}=K\left(1+\frac{m}{N}\right)$$ है। बहुत अधिक $$N\left(>10^{3}\right)$$ के लिए धारिता $$C=\alpha\left(\frac{K \epsilon_{0} A}{d \ln 2}\right)$$ है | $$\alpha$$ का मान __________ होगा |

[मुक्त आकाश (free space) की वैद्युतशीलता $$\epsilon_{0}$$ है ]

एक $$L$$ लंबाई तथा $$W$$ चौड़ाई की एक समतल संरचना दो भित्न प्रकाशीय पदार्थों से बनी है, जिनका अपवर्तनांक $$n_{1}=1.5$$ और $$n_{2}=1.44$$ है, जैसा चित्र में प्रदर्शित है | यदि $$L \gg W$$ है तब $$A B$$ सिरे पर आपतित किरण का $$C D$$ सिरे से उदगमन (emerge) संरचना के अंदर पूर्ण आंतरिक परावर्तन (total internal reflection) होने पर ही होगा | $$L=9.6 \mathrm{~m}$$ के लिए, यदि आपतन कोण $$\theta$$ को बदलते हैं तब किरण द्वारा $$\mathrm{CD}$$ सिरे से बाहर निकलने में लिया गया अधिकतम समय $$t \times 10^{-9} \mathrm{~s}$$ है, जहाँ $$t$$ का मान __________ है।

[ प्रकाश कि गति, $$c=3 \times 10^{8} \mathrm{~m} / \mathrm{s}$$ ]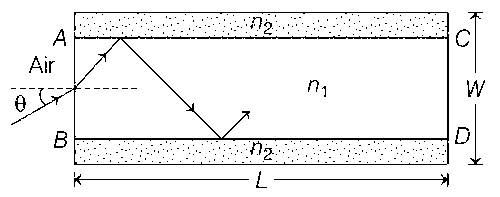

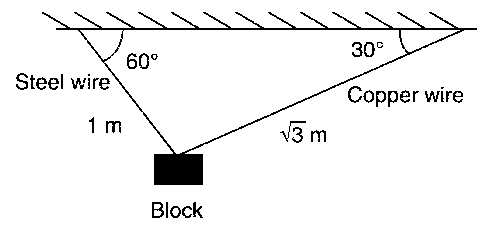
एक $$100 \mathrm{~N}$$ भार वाले गुटके को तांबे और स्टील के तारों, जिनका अनुप्रस्थ काट क्षेत्रफल (cross sectional area) एकसमान तथा $$0.5 \mathrm{~cm}^{2}$$ है और लंबाई क्रमशः $$\sqrt{3} \mathrm{~m}$$ तथा $$1 \mathrm{~m}$$ है, द्वारा लटकाया जाता है । तारों के दूसरे छोर छत पर चित्रानुसार जुड़े हुए हैं । तांबे और स्टील के तार क्रमशः छत से $$30^{\circ}$$ और $$60^{\circ}$$ का कोण बनाते हैं। यदि तांबे के तार में लंबाई वृद्धि $$\left(\Delta l_{C}\right)$$ तथा स्टील के तार में लंबाई वृद्धि $$\left(\Delta l_{S}\right)$$ है तब $$\frac{\Delta l_{C}}{\Delta l_{S}}=$$ __________ है ।

[तांबे और स्टील का यंग गुणांक (Young's modulus) क्रमशः $$1 \times 10^{11} \mathrm{~N} / \mathrm{m}^{2}$$ and $$2 \times 10^{11} \mathrm{~N} / \mathrm{m}^{2}$$ हैं ]

एक $$30^{\circ} \mathrm{C}$$ के द्रव को एक ऊष्मामापी (calorimeter), जिसका तापमान $$110^{\circ} \mathrm{C}$$, में धीरे-धीरे डाला जाता है । द्रव का कथनांक (boiling temperature) $$80^{\circ} \mathrm{C}$$ है | ऐसा पाया गया कि द्रव का पहला $$5~\mathrm{gm}$$ पूर्ण रूप से वाष्पित हो जाता है । इसके बाद द्रव की $$80 ~\mathrm{gm}$$ और मात्रा डालने पर साम्यावस्था का तापमान $$50^{\circ} \mathrm{C}$$ हो जाता है । द्रव की गुप्त (latent) और विशिष्ट (specific) ऊष्माओं का अनुपात _____________ $${ }^{\circ} \mathrm{C}$$ होगा।

[ वातावरण के साथ ऊष्मा स्थानांतरण को उपेक्षणीय माने ]

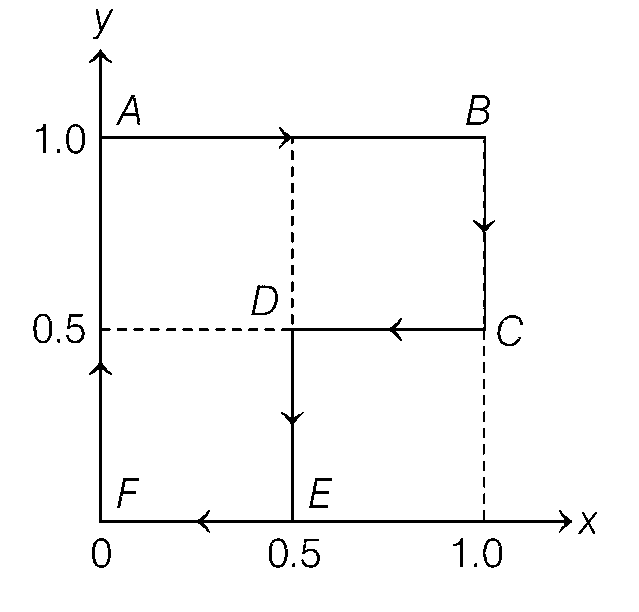
एक कण को बल $$\vec{F}=(\alpha y \hat{\imath}+2 \alpha x \hat{\jmath}) ~\mathrm{N}$$, जहाँ $$x$$ और $$y$$ का मान मीटर में हैं तथा $$\alpha=-1 ~\mathrm{Nm}^{-1}$$ है, की उपस्थिति में $$\mathrm{AB}-\mathrm{BC}-C D-D E-E F-F A$$ पथ पर चित्रानुसार चलाया जाता है। बल $$\vec{F}$$ द्वारा कण पर किये गये कार्य का परिमाण ____________ जूल (Joule) होगा।

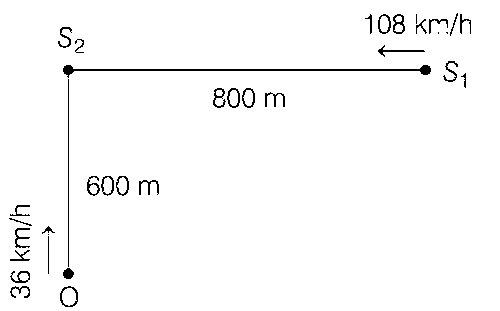
15 एक रेलगाड़ी (S1) $$108 \mathrm{~km} / \mathrm{h}$$ के समान वेग से चलते हुए दूसरी रेलगाड़ी (S2) जो कि स्टेशन पर खड़ी है, की तरफ जा रही है । एक श्रोता $$(\mathrm{O}) 36 \mathrm{~km} / \mathrm{h}$$ के समान वेग से $$\mathrm{S} 2$$ की तरफ चित्रानुसार जा रहा है । दोनों रेलगाडियाँ $$120 \mathrm{~Hz}$$ के समान आवृत्ति की सीटियाँ बजा रही हैं। जब $$O$$ की दूरी $$\mathrm{S} 2$$ से $$600 \mathrm{~m}$$ है तथा $$\mathrm{S} 1$$ और $$\mathrm{S} 2$$ के बीच की दूरी $$800 \mathrm{~m}$$ है तब $$\mathrm{O}$$ के द्वारा सुने गए विस्पंदनों (beats) की संख्या ______________ है।

[ध्वनि की गति $$=330 \mathrm{~m} / \mathrm{s}$$ ]