JEE Advance - Physics Hindi (2019 - Paper 1 Offline - No. 6)
चित्रानुसार एक असमान चुंबकीय क्षेत्र $$\vec{B}=B_{0}\left(1+\left(\frac{y}{L}\right)^{\beta}\right) \hat{k}$$ में एक परवलयाकार (parabolic shape), आरंभ में $$y=x^{2}$$ वाला, विद्युत चालक तार वेग $$\vec{V}=V_{0} \hat{\imath}$$ से चल रहा है । यदि $$V_{0}, B_{0}, L$$ तथा $$\beta$$ धनात्मक नियतांक हैं एवं तार के सिरों के मध्य उत्पत्र विभवांतर $$\Delta \phi$$ है, तब निम्नलिखित कथनों में से कौन सा(से) सही है(हैं) ?
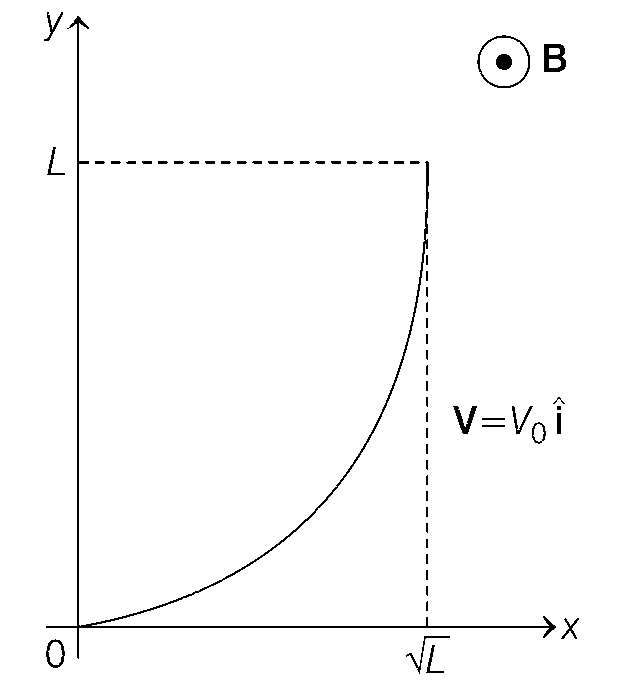
$$\beta=2$$ के लिए, $$|\Delta \phi|=\frac{4}{3} B_{0} V_{0} L$$
यदि इस परवलयाकार तार के स्थान पर $$\sqrt{2} L$$ लंबाई वाला एक सीधे तार, आरम्भ में $$y=x$$, का उपयोग किया जाये तब $$|\Delta \phi|$$ समान रहेगा।
$$\beta=0$$ के लिए, $$|\Delta \phi|=\frac{1}{2} B_{0} V_{0} L$$
$$|\Delta \phi|$$ का मान $$y$$-अक्ष पर तार की प्रेक्षेपित लंबाई के समानुपाती होगा।
Comments (0)


