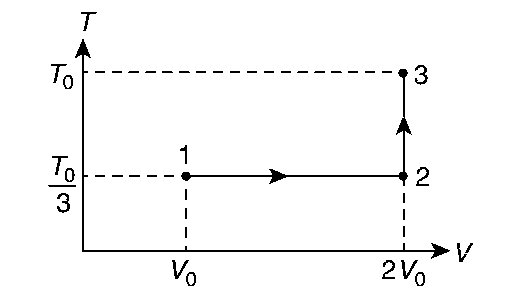
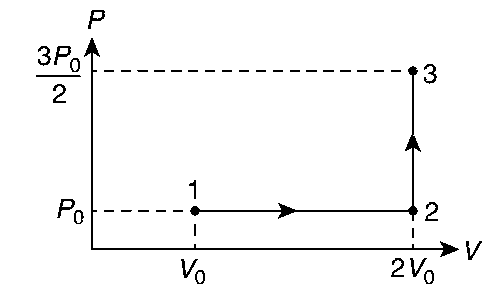
JEE Advance - Physics (2019 - Paper 2 Offline)
1
An electric dipole with dipole moment $${{{p_0}} \over {\sqrt 2 }}(\widehat i + \widehat j)$$ is held fixed at the origin O in the presence of a uniform electric field of magnitude E0.
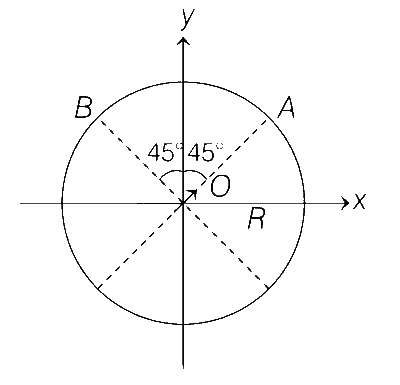
If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are, ($$ \in $$0 is the permittivity of the free space, R >> dipole size)

If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are, ($$ \in $$0 is the permittivity of the free space, R >> dipole size)
Answer
B
C
2
A small particle of mass m moving inside a heavy, hollow and straight tube along the tube axis undergoes elastic collision at two ends. The tube has no friction and it is closed at one end by a flat surface while the other end is fitted with a heavy movable flat piston as shown in figure.

When the distance of the piston from closed end is L = L0, the particle speed is v = v0. The piston is moved inward at a very low speed V such that $$V < < {{dL} \over L}{v_0}$$, where dL is the infinitesimal displacement of the piston. Which of the following statement(s) is/are correct?

When the distance of the piston from closed end is L = L0, the particle speed is v = v0. The piston is moved inward at a very low speed V such that $$V < < {{dL} \over L}{v_0}$$, where dL is the infinitesimal displacement of the piston. Which of the following statement(s) is/are correct?
Answer
A
C
3
Three glass cylinders of equal height H = 30 cm and same refractive index n = 1.5 are placed on a horizontal surface as shown in figure.
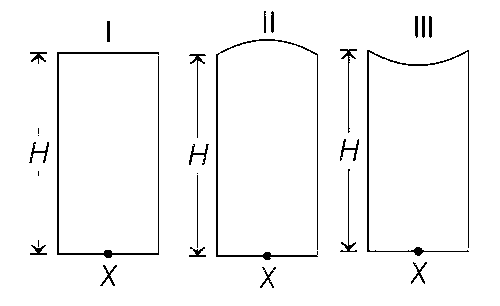
Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (R = 3 m). If H1, H2, and H3 are the apparent depths of a point X on the bottom of the three cylinders, respectively, the correct statement(s) is/are

Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (R = 3 m). If H1, H2, and H3 are the apparent depths of a point X on the bottom of the three cylinders, respectively, the correct statement(s) is/are
Answer
A
D
4
A block of mass 2M is attached to a massless spring with spring-constant k.This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1, a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0. Which of the following option(s) is/are correct? [g is the acceleration due to gravity. Neglect friction]
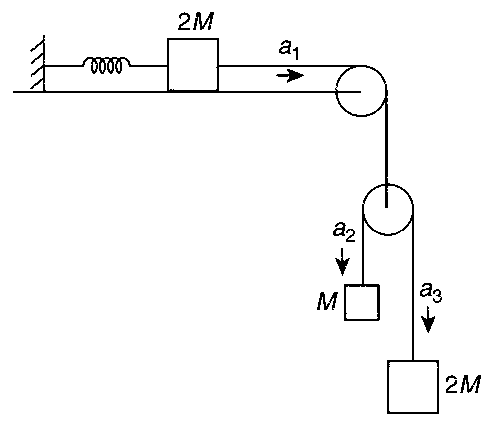

Answer
(A)
$${a_2} - {a_1} = {a_1} - {a_3}$$
5
A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is/are correct, when the rod makes an angle 60$$^\circ $$ with vertical? [g is the acceleration due to gravity]
Answer
B
C
D
6
In a Young's double slit experiment, the slit separation d is 0.3 mm and the screen distance D is 1 m. A parallel beam of light of wavelength 600 nm is incident on the slits at angle $$\alpha $$ as shown in figure.

On the screen, the point O is equidistant from the slits and distance PO is 11.0 mm. Which of the following statement(s) is/are correct?

On the screen, the point O is equidistant from the slits and distance PO is 11.0 mm. Which of the following statement(s) is/are correct?
Answer
(B)
For $$\alpha = {{0.36} \over \pi }$$ degree, there will be destructive interference at point P.
7
A free hydrogen atom after absorbing a photon of wavelength $$\lambda $$a gets excited from the state n = 1 to the state n = 4. Immediately after that the electron jumps to n = m state by emitting a photon of wavelength $$\lambda $$e. Let the change in momentum of atom due to the absorption and the emission be $$\Delta {p_a}$$ and $$\Delta {p_e}$$, respectively. If $${{{\lambda _a}} \over {{\lambda _e}}} = {1 \over 5}$$, which of the option(s) is/are correct? [Use hc = 1242 eVnm; 1 nm = 10-9 m, h and c are Planck's constant and speed of light in vacuum, respectively]
Answer
A
B
8
A mixture of ideal gas containing 5 moles of monatomic gas and 1 mole of rigid diatomic gas is initially at pressure P0, volume V0, and temperature T0. If the gas mixture is adiabatically compressed to a volume $${{{V_0}} \over 4}$$, then the correct statement(s) is/are
(Given, 21.2 = 2.3; 23.2 = 9.2; R is a gas constant)
(Given, 21.2 = 2.3; 23.2 = 9.2; R is a gas constant)
Answer
A
C
D
9
Suppose a $$_{88}^{226}Ra$$ nucleus at rest and in ground state undergoes $$\alpha $$-decay to a $$_{86}^{222}Rn$$ nucleus in its excited state. The kinetic energy of the emitted $$\alpha $$ particle is found to be 4.44 MeV. $$_{86}^{222}Rn$$ nucleus then goes to its ground state by $$\gamma $$-decay. The energy of the emitted $$\gamma $$ photon is ............ keV.
[Given : atomic mass of $$_{86}^{226}Ra$$ = 226.005 u, atomic of $$_{86}^{222}Rn$$ = 222.000 u, atomic mass of $$\alpha $$ particle = 4.000 u, 1 u = 931 MeV/e2, c is speed of the light]
[Given : atomic mass of $$_{86}^{226}Ra$$ = 226.005 u, atomic of $$_{86}^{222}Rn$$ = 222.000 u, atomic mass of $$\alpha $$ particle = 4.000 u, 1 u = 931 MeV/e2, c is speed of the light]
Answer
135
10
A monochromatic light is incident from air on a refracting surface of a prism of angle 75$$^\circ $$ and refractive index $${n_0} = \sqrt 3 $$. The other refracting surface of the prism is coated by a thin film of material of refractive index n as shown in figure. The light suffers total internal reflection at the coated prism surface for an incidence angle of $$\theta \le 60^\circ $$. The value of n2 is .............
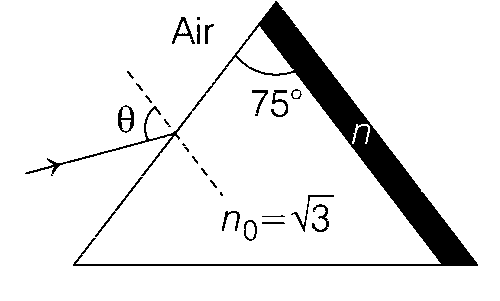

Answer
1.50
11
A perfectly reflecting mirror of mass M mounted on a spring constitutes a spring-mass system of angular frequency $$\Omega $$ such that $${{4\pi M\Omega } \over h} = {10^{24}}{m^{ - 2}}$$ with h as Planck's constant. N photons of wavelength $$\lambda $$ = 8$$\pi $$ $$ \times $$ 10$$ - $$6 m strike the mirror simultaneously at normal incidence such that the mirror gets displaced by 1 $$\mu $$m. If the value of N is x $$ \times $$ 1012, then the value of x is ................ [Consider the spring as massless]


Answer
1.0
12
An optical bench has 1.5 m long scale having four equal divisions in each cm. While measuring the focal length of a convex lens, the lens is kept at 75 cm mark of the scale and the object pin is kept at 45 cm mark. The image of the object pin on the other side of the lens overlaps with image pin that is kept at 135 cm mark. In this experiment, the percentage error in the measurement of the focal length of the lens is ..............
Answer
1.38
13
A ball is thrown from ground at an angle $$\theta $$ with horizontal and with an initial speed u0. For the resulting projectile motion, the magnitude of average velocity of the ball up to the point when it hits the ground for the first time is V1. After hitting the ground, the ball rebounds at the same angle $$\theta $$ but with a reduced speed of $${{{u_0}} \over \alpha }$$. Its motion continues for a long time as shown in figure. If the magnitude of average velocity of the ball for entire duration of motion is 0.8 V1, the value of $$\alpha $$ is ..................


Answer
4.0
14
A 10 cm long perfectly conducting wire PQ is moving with a velocity I cm/s on a pair of horizontal rails of zero resistance. One side of the rails is connected to an inductor L = 1 mH and a resistance R = 1$$\Omega $$ as shown in figure. The horizontal rails, L and R lie in the same plane with a uniform magnetic field B = 1 T perpendicular to the plane. If the key S is closed at certain instant, the current in the circuit after 1 millisecond is x $$ \times $$ 10-3 A, where the value of x is ...........
[Assume the velocity of wire PQ remains constant (1 cm/s) after key S is closed. Given e-1 = 0.37, where e is base of the natural logarithm]
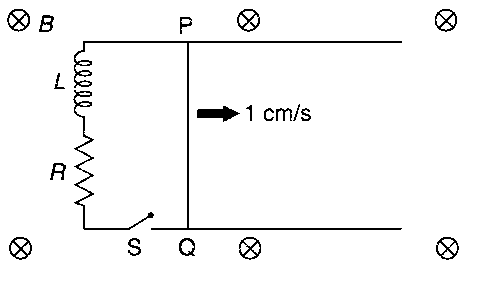
[Assume the velocity of wire PQ remains constant (1 cm/s) after key S is closed. Given e-1 = 0.37, where e is base of the natural logarithm]

Answer
0.63
15
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length $$\mu $$, 2$$\mu $$, 3$$\mu $$ and 4$$\mu $$ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1$$\mu $$ at free length L0 and tension T0 the fundamental mode frequency is f0.
List-I gives the above four strings while list-II lists the magnitude of some quantity.
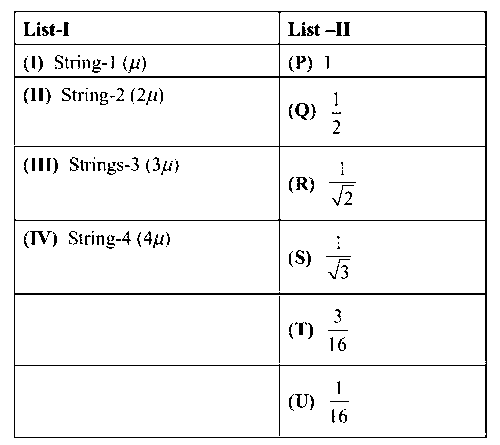
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be
List-I gives the above four strings while list-II lists the magnitude of some quantity.

If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be
Answer
(B)
I $$ \to $$ P, II $$ \to $$ R, III $$ \to $$ S, IV $$ \to $$ Q
16
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length $$\mu $$, 2$$\mu $$, 3$$\mu $$ and 4$$\mu $$ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1$$\mu $$ at free length L0 and tension T0 the fundamental mode frequency is f0.
List-I gives the above four strings while list-II lists the magnitude of some quantity.
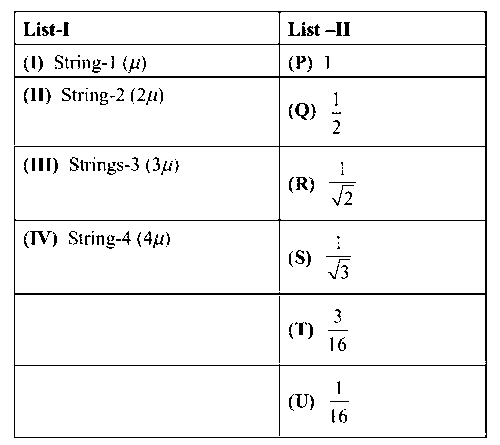
The length of the strings 1, 2, 3 and 4 are kept fixed at L0, $${{3{L_0}} \over 2}$$, $${{5{L_0}} \over 4}$$ and $${{7{L_0}} \over 4}$$ respectively. Strings 1, 2, 3 and 4 are vibrated at their 1st, 3rd, 5th and 14th harmonies, respectively such that all the strings have same frequency.
The correct match for the tension in the four strings in the units of T0 will be
List-I gives the above four strings while list-II lists the magnitude of some quantity.

The length of the strings 1, 2, 3 and 4 are kept fixed at L0, $${{3{L_0}} \over 2}$$, $${{5{L_0}} \over 4}$$ and $${{7{L_0}} \over 4}$$ respectively. Strings 1, 2, 3 and 4 are vibrated at their 1st, 3rd, 5th and 14th harmonies, respectively such that all the strings have same frequency.
The correct match for the tension in the four strings in the units of T0 will be
Answer
(C)
I $$ \to $$ P, II $$ \to $$ Q, III $$ \to $$ T, IV $$ \to $$ U