Sign In

JEE Advance - Physics (2019 - Paper 2 Offline - No. 18)

In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by T$$\Delta $$X where T is temperature of the system and $$\Delta $$X is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas, $$X = {3 \over 2}R\,\ln \left( {{T \over {{T_A}}}} \right) + R\,\ln \left( {{V \over {{V_A}}}} \right)$$

Here, R is gas constant, V is volume of gas, TA and VA are constants.

The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by T$$\Delta $$X where T is temperature of the system and $$\Delta $$X is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas, $$X = {3 \over 2}R\,\ln \left( {{T \over {{T_A}}}} \right) + R\,\ln \left( {{V \over {{V_A}}}} \right)$$

Here, R is gas constant, V is volume of gas, TA and VA are constants.

The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

In a thermodynamic process on an ideal monatomic gas, the infinitesimal heat absorbed by the gas is given by T$$\Delta $$X where T is temperature of the system and $$\Delta $$X is the infinitesimal change in a thermodynamic quantity X of the system. For a mole of monatomic ideal gas, $$X = {3 \over 2}R\,\ln \left( {{T \over {{T_A}}}} \right) + R\,\ln \left( {{V \over {{V_A}}}} \right)$$

Here, R is gas constant, V is volume of gas, TA and VA are constants.

The List-I below gives some quantities involved in a process and List-II gives some possible values of these quantities.

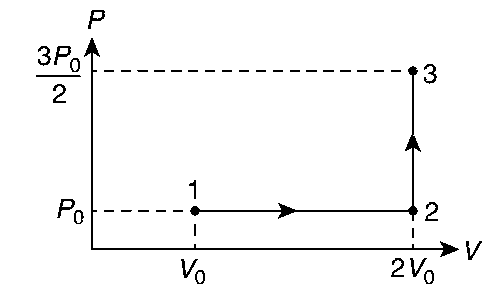
If the process carried out on one mole of monoatomic ideal gas is as shown in the PV-diagram with $${p_0}{V_0} = {1 \over 3}R{T_0}$$, the correct match is,

JEE Advanced 2019 Paper 2 Offline Physics - Heat and Thermodynamics Question 40 English
I$$ \to $$S, II $$ \to $$ R, III $$ \to $$ Q, IV $$ \to $$ T
I $$ \to $$ Q, II $$ \to $$ R, III $$ \to $$ P, IV $$ \to $$ U
I $$ \to $$ Q, II $$ \to $$ S, III $$ \to $$ R, IV $$ \to $$ U
I $$ \to $$ Q, II $$ \to $$ R, III $$ \to $$ S, IV $$ \to $$ U

Explanation

(I) $${W_{1 \to 2 \to 3}} = {W_{1 \to 2}} + {W_{2 \to 3}} = {P_0}[2{V_0} - {V_0}] + 0 = {P_0}{V_0}$$

$${W_{1 \to 2 \to 3}} = {P_0}{V_0} = {{R{T_0}} \over 3}$$ (I$$ \to $$Q)

$${U_{1 \to 2 \to 3}} = {3 \over 2}\left[ {{{3{P_0}} \over 2} \times 2{V_0} - {P_0}{V_0}} \right] = {3 \over 2} \times 2{P_0}{V_0} = 3{P_0}{V_0} = R{T_0}$$(II$$ \to $$R)

(III) $${Q_{1 \to 2 \to 3}} = {U_{1 \to 2 \to 3}} + {W_{1 \to 2 \to 3}} = R{T_0} + {{R{T_0}} \over 3} = {{4R{T_0}} \over 3}$$(III$$ \to $$S)

(IV) $${Q_{1 \to 2}} = n{C_p}\Delta T = n{5 \over 2}R({T_2} - {T_1}) = {5 \over 2}[{P_0}2{V_0} - {P_0}{V_0}] = {5 \over 2}{P_0}{V_0} = {5 \over 2}{{R{T_0}} \over 3} = {5 \over 6}{R_0}{T_0}$$ (IV$$ \to $$U)

Comments (0)

Advertisement