JEE Advance - Physics (2019 - Paper 2 Offline - No. 1)
An electric dipole with dipole moment $${{{p_0}} \over {\sqrt 2 }}(\widehat i + \widehat j)$$ is held fixed at the origin O in the presence of a uniform electric field of magnitude E0.
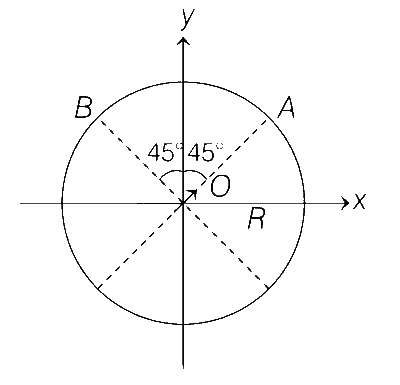
If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are, ($$ \in $$0 is the permittivity of the free space, R >> dipole size)

If the potential is constant on a circle of radius R centered at the origin as shown in figure, then the correct statement(s) is/are, ($$ \in $$0 is the permittivity of the free space, R >> dipole size)
The magnitude of total electric field on any two points of the circle will be same.
Total electric field at point B is $${\overrightarrow E _B}$$ = 0
$$R = {\left( {{{{p_0}} \over {4\pi { \in _0}{E_0}}}} \right)^{1/3}}$$
Total electric field at point A is
$${\overrightarrow E _A} = \sqrt 2 {E_0}(\widehat i + \widehat j)$$
$${\overrightarrow E _A} = \sqrt 2 {E_0}(\widehat i + \widehat j)$$
Explanation
R >> Dipole size.
Circle is equipotential.
So, Enet should be perpendicular to surface hence,
$${{k{p_0}} \over {{r^3}}} = {E_0}$$
$$ \Rightarrow $$ $$R = {\left( {{{k{p_0}} \over {{E_0}}}} \right)^{1/3}}$$
At point B, net electric field will be zero.
EB = 0
$${({E_A})_{net}} = {{2k{p_0}} \over {{R^3}}} + {E_0} = 3{E_0}$$
Electric field at point A, $${E_A} = {3 \over {\sqrt 2 }}{E_0}[\widehat i + \widehat j]$$
$${({E_B})_{net}}$$ = 0
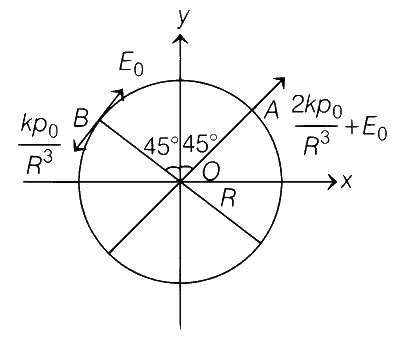
Circle is equipotential.
So, Enet should be perpendicular to surface hence,
$${{k{p_0}} \over {{r^3}}} = {E_0}$$
$$ \Rightarrow $$ $$R = {\left( {{{k{p_0}} \over {{E_0}}}} \right)^{1/3}}$$
At point B, net electric field will be zero.
EB = 0
$${({E_A})_{net}} = {{2k{p_0}} \over {{R^3}}} + {E_0} = 3{E_0}$$
Electric field at point A, $${E_A} = {3 \over {\sqrt 2 }}{E_0}[\widehat i + \widehat j]$$
$${({E_B})_{net}}$$ = 0

Comments (0)


