JEE Advance - Physics (2019 - Paper 2 Offline - No. 16)
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length $$\mu $$, 2$$\mu $$, 3$$\mu $$ and 4$$\mu $$ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1$$\mu $$ at free length L0 and tension T0 the fundamental mode frequency is f0.
List-I gives the above four strings while list-II lists the magnitude of some quantity.
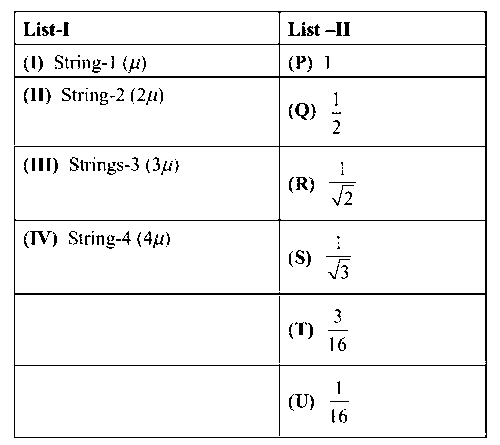
The length of the strings 1, 2, 3 and 4 are kept fixed at L0, $${{3{L_0}} \over 2}$$, $${{5{L_0}} \over 4}$$ and $${{7{L_0}} \over 4}$$ respectively. Strings 1, 2, 3 and 4 are vibrated at their 1st, 3rd, 5th and 14th harmonies, respectively such that all the strings have same frequency.
The correct match for the tension in the four strings in the units of T0 will be
List-I gives the above four strings while list-II lists the magnitude of some quantity.

The length of the strings 1, 2, 3 and 4 are kept fixed at L0, $${{3{L_0}} \over 2}$$, $${{5{L_0}} \over 4}$$ and $${{7{L_0}} \over 4}$$ respectively. Strings 1, 2, 3 and 4 are vibrated at their 1st, 3rd, 5th and 14th harmonies, respectively such that all the strings have same frequency.
The correct match for the tension in the four strings in the units of T0 will be
I $$ \to $$ P, II $$ \to $$ R, III $$ \to $$ T, IV $$ \to $$ U
I $$ \to $$ P, II $$ \to $$ Q, III $$ \to $$ R, IV $$ \to $$ T
I $$ \to $$ P, II $$ \to $$ Q, III $$ \to $$ T, IV $$ \to $$ U
I $$ \to $$ T, II $$ \to $$ Q, III $$ \to $$ R, IV $$ \to $$ U
Explanation
Case 1. $$L = {L_0},\,T = {T_0},\,f = {f_0}$$
$${f_1} = {1 \over {2{L_0}}}\sqrt {{{{T_0}} \over \mu }} $$
Case 2. $$L = {{3{L_0}} \over 2}$$
$${f_2} = {3 \over {2 \times {{3{L_0}} \over 2}}}\sqrt {{{{T_2}} \over {2\mu }}} = {f_0}$$
$$ \Rightarrow {f_0} = {1 \over {2{L_0}}}\sqrt {{{{T_2}} \over \mu }} \Rightarrow {T_2} = {{{T_0}} \over 2}$$
Case 3. $$L = {{5{L_0}} \over 4}$$
$${f_3} = {5 \over {2 \times {{5{L_0}} \over 4}}}\sqrt {{{{T_3}} \over {3\mu }}} = {f_0}$$
$$ \Rightarrow {f_0} = {2 \over {\sqrt 3 {L_0}}}\sqrt {{{{T_3}} \over \mu }} \Rightarrow {T_3} = {{3{T_0}} \over {16}}$$
Case 4. $$L = {{7{L_0}} \over 4}$$
$${f_4} = {{14} \over {2 \times {{7{L_0}} \over 4}}}\sqrt {{{{T_4}} \over {4\mu }}} = {f_0}$$
$$ \Rightarrow {f_0} = {2 \over {{L_0}}}\sqrt {{{{T_4}} \over \mu }} \Rightarrow {T_4} = {{{T_0}} \over {16}}$$
$${f_1} = {1 \over {2{L_0}}}\sqrt {{{{T_0}} \over \mu }} $$
Case 2. $$L = {{3{L_0}} \over 2}$$
$${f_2} = {3 \over {2 \times {{3{L_0}} \over 2}}}\sqrt {{{{T_2}} \over {2\mu }}} = {f_0}$$
$$ \Rightarrow {f_0} = {1 \over {2{L_0}}}\sqrt {{{{T_2}} \over \mu }} \Rightarrow {T_2} = {{{T_0}} \over 2}$$
Case 3. $$L = {{5{L_0}} \over 4}$$
$${f_3} = {5 \over {2 \times {{5{L_0}} \over 4}}}\sqrt {{{{T_3}} \over {3\mu }}} = {f_0}$$
$$ \Rightarrow {f_0} = {2 \over {\sqrt 3 {L_0}}}\sqrt {{{{T_3}} \over \mu }} \Rightarrow {T_3} = {{3{T_0}} \over {16}}$$
Case 4. $$L = {{7{L_0}} \over 4}$$
$${f_4} = {{14} \over {2 \times {{7{L_0}} \over 4}}}\sqrt {{{{T_4}} \over {4\mu }}} = {f_0}$$
$$ \Rightarrow {f_0} = {2 \over {{L_0}}}\sqrt {{{{T_4}} \over \mu }} \Rightarrow {T_4} = {{{T_0}} \over {16}}$$
Comments (0)


