JEE Advance - Physics (2019 - Paper 2 Offline - No. 4)
A block of mass 2M is attached to a massless spring with spring-constant k.This block is connected to two other blocks of masses M and 2M using two massless pulleys and strings. The accelerations of the blocks are a1, a2 and a3 as shown in the figure. The system is released from rest with the spring in its unstretched state. The maximum extension of the spring is x0. Which of the following option(s) is/are correct? [g is the acceleration due to gravity. Neglect friction]
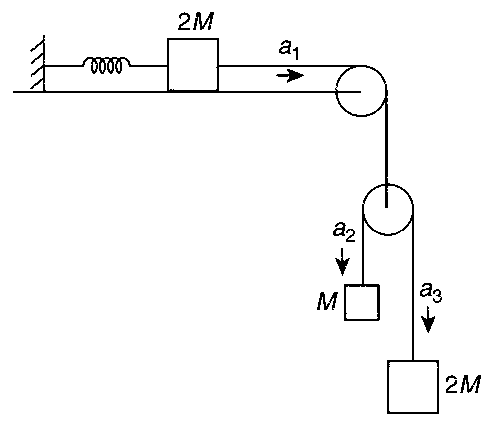

$${a_2} - {a_1} = {a_1} - {a_3}$$
At an extension of $${{{x_0}} \over 4}$$ of the spring, the magnitude of acceleration of the block connected to the spring is $${{3g} \over {10}}$$.
$${x_0} = {{4Mg} \over k}$$
When spring achieves an extension of $${{{x_0}} \over 2}$$ for the first time, the speed of the block connected to the spring is $$3g\sqrt {{M \over {5k}}} $$
Explanation
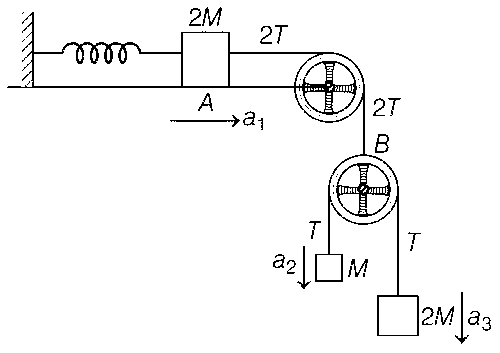
In the frame of pulley B,
the hanging masses have accelerations :
$$M \to ({a_2} - {a_1})$$
$$2M \to ({a_3} - {a_1})$$ : downward.
$$ \therefore $$ $$({a_2} - {a_1})$$ = $$( - {a_3} - {a_1})$$ [constant]
Assuming that the extension of the spring is x
We consider the FBD of A :
$$2M.{{{d^2}x} \over {d{t^2}}} = 2T - kx$$

where, $${a_1} \equiv {{{d^2}x} \over {d{t^2}}}$$ ....(i)
and the FBD of the rest of the system in the frame of pulley B :
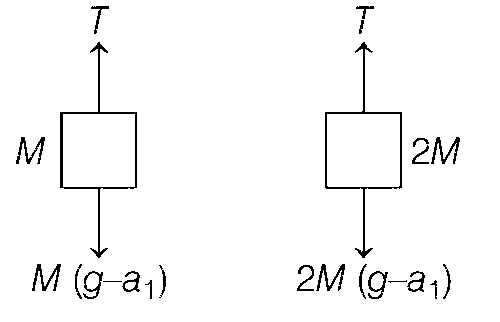
Upward acceleration of block M w.r.t. the pulley B = Downward acceleration of block 2M w.r.t. the pulley.
$${{T - M(g - {a_1})} \over M} = {{2M(g - {a_1}) - T} \over {2M}}$$
$$ \Rightarrow T = {{4M} \over 3}(g - {a_1})$$ .....(ii)
Substituting in Eq. (i), we get
$$2M.{a_1} = {{8M} \over 3}(g - {a_1}) - kx$$
or $${{14M} \over 3}{a_1} = {{8Mg} \over 3} - kx$$ ....(iii)
This is equation of SHM
Maximum extension = 2 $$ \times $$ amplitude
i.e., $${x_0} = 2 \times {{8Mg} \over {3k}}$$
Amplitude = $${{{x_0}} \over 2} = {{3Mg} \over {3k}}$$ and $$\omega = \sqrt {{{3k} \over {14M}}} $$
At $${{{x_0}} \over 4}$$, acceleration is easily found from Eq. (iii),
$${{14M} \over 3}{a_1} = {{8Mg} \over 3} - {{4Mg} \over 3}$$
$${a_1} = {{2g} \over 7}$$
At $${{{x_0}} \over 2}$$, speed of the block
$$(2M) = \omega \times \,amplitude$$
= $$\sqrt {{{3k} \over {14M}}} \times {{8Mg} \over {3k}}$$
$$ \therefore $$ option (a) is correct.
Comments (0)


