JEE Advance - Physics (2019 - Paper 2 Offline - No. 15)
A musical instrument is made using four different metal strings, 1, 2, 3 and 4 with mass per unit length $$\mu $$, 2$$\mu $$, 3$$\mu $$ and 4$$\mu $$ respectively. The instrument is played by vibrating the strings by varying the free length in between the range L0 and 2L0. It is found that in string-1$$\mu $$ at free length L0 and tension T0 the fundamental mode frequency is f0.
List-I gives the above four strings while list-II lists the magnitude of some quantity.
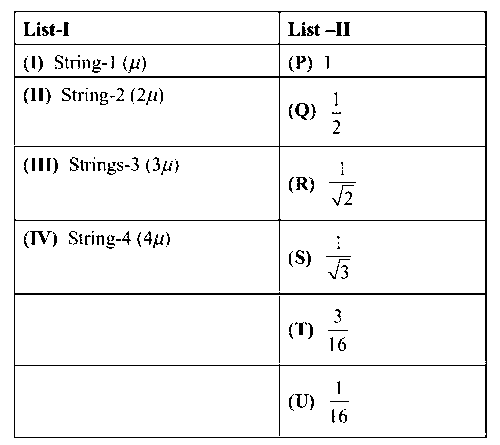
If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be
List-I gives the above four strings while list-II lists the magnitude of some quantity.

If the tension in each string is T0, the correct match for the highest fundamental frequency in f0 units will be
I $$ \to $$ P, II $$ \to $$ Q, III $$ \to $$ T, IV $$ \to $$ S
I $$ \to $$ P, II $$ \to $$ R, III $$ \to $$ S, IV $$ \to $$ Q
I $$ \to $$ Q, II $$ \to $$ S, III $$ \to $$ R, IV $$ \to $$ P
I $$ \to $$ Q, II $$ \to $$ P, III $$ \to $$ R, IV $$ \to $$ T
Explanation
Fundamental frequency is maximum when length is minimum i.e. L0,
Case 1. $$L = {L_0},\,T = {T_0},\,f = {f_0}$$;
$${f_1} = {1 \over {2{L_0}}}\sqrt {{{{T_0}} \over \mu }} $$
Case 2. $${f_2} = {1 \over {{L_0}}}\sqrt {{{{T_2}} \over {2\mu }}} = {{{f_0}} \over {\sqrt 2 }}$$
Case 3. $${f_3} = {1 \over {{L_0}}}\sqrt {{{{T_2}} \over {3\mu }}} = {{{f_0}} \over {\sqrt 3 }}$$
Case 4. $${f_4} = {1 \over {{L_0}}}\sqrt {{{{T_2}} \over {4\mu }}} = {{{f_0}} \over 2}$$
Case 1. $$L = {L_0},\,T = {T_0},\,f = {f_0}$$;
$${f_1} = {1 \over {2{L_0}}}\sqrt {{{{T_0}} \over \mu }} $$
Case 2. $${f_2} = {1 \over {{L_0}}}\sqrt {{{{T_2}} \over {2\mu }}} = {{{f_0}} \over {\sqrt 2 }}$$
Case 3. $${f_3} = {1 \over {{L_0}}}\sqrt {{{{T_2}} \over {3\mu }}} = {{{f_0}} \over {\sqrt 3 }}$$
Case 4. $${f_4} = {1 \over {{L_0}}}\sqrt {{{{T_2}} \over {4\mu }}} = {{{f_0}} \over 2}$$
Comments (0)


