JEE Advance - Physics (2019 - Paper 2 Offline - No. 6)
In a Young's double slit experiment, the slit separation d is 0.3 mm and the screen distance D is 1 m. A parallel beam of light of wavelength 600 nm is incident on the slits at angle $$\alpha $$ as shown in figure.

On the screen, the point O is equidistant from the slits and distance PO is 11.0 mm. Which of the following statement(s) is/are correct?

On the screen, the point O is equidistant from the slits and distance PO is 11.0 mm. Which of the following statement(s) is/are correct?
For $$\alpha $$ = 0, there will be constructive interference at point P.
For $$\alpha = {{0.36} \over \pi }$$ degree, there will be destructive interference at point P.
For $$\alpha $$ = $$\alpha = {{0.36} \over \pi }$$ degree, there will be destructive interference at point O.
Fringe spacing depends on $$\alpha $$.
Explanation
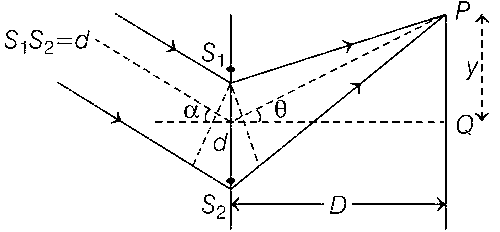
$$\Delta $$x = d sin$$\alpha $$ + d sin$$\theta $$
$$\theta $$ and $$\alpha $$ are small angles
$$ \therefore $$ $$\Delta $$x = d$$\alpha $$ + $${{dy} \over D}$$
(a) $$\alpha $$ = 0
$$ \therefore $$ $$\Delta $$$$x = {{dy} \over D} = {{0.3 \times 11} \over {1000}} = 33 \times {10^{ - 4}}$$ mm
$$\Delta $$x in terms of $$\lambda $$ = $${{33 \times {{10}^{ - 4}}} \over {600 \times {{10}^{ - 6}}}}\lambda = {{11\lambda } \over 2}$$
as $$\Delta x = (2n - 1){\lambda \over 2}$$
There will be destructive interference.
(b) $$\Delta x = 0.3\,mm \times {{0.36} \over \pi } \times {\pi \over {180}} + {{0.3\,mm \times 11\,mm} \over {1000}}$$
$$ = 39 \times {10^{ - 4}}$$ mm
$$39 \times {10^{ - 4}}$$ = $$(2x - 1) \times {{600 \times {{10}^{ - 9}} \times {{10}^{ - 3}}} \over 2}$$
n = 7
So, there will be destruction interference.
(c) $$\Delta x = 3\,mm \times {{0.36} \over \pi } \times {\pi \over {180}} + 0$$ = 600 nm
600 nm = n$$\lambda $$ $$ \Rightarrow $$ n = 1
So, there will be construction interference.
(d) Fringe width does not depend on $$\alpha $$.
Comments (0)


