JEE Advance - Physics (2019 - Paper 2 Offline - No. 14)
A 10 cm long perfectly conducting wire PQ is moving with a velocity I cm/s on a pair of horizontal rails of zero resistance. One side of the rails is connected to an inductor L = 1 mH and a resistance R = 1$$\Omega $$ as shown in figure. The horizontal rails, L and R lie in the same plane with a uniform magnetic field B = 1 T perpendicular to the plane. If the key S is closed at certain instant, the current in the circuit after 1 millisecond is x $$ \times $$ 10-3 A, where the value of x is ...........
[Assume the velocity of wire PQ remains constant (1 cm/s) after key S is closed. Given e-1 = 0.37, where e is base of the natural logarithm]
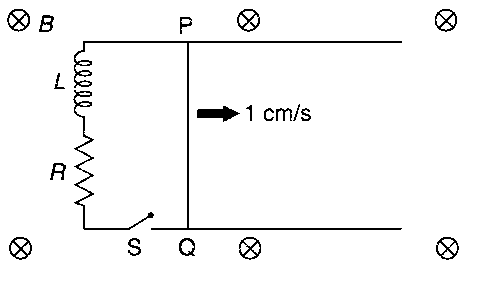
[Assume the velocity of wire PQ remains constant (1 cm/s) after key S is closed. Given e-1 = 0.37, where e is base of the natural logarithm]

Answer
0.63
Explanation
Motional emf,
$$e = (v \times B)dl = {10^{ - 2}} \times 1 \times {10^{ - 1}}$$
e = $${10^{ - 3}}V$$
$${\tau _L} = LR = ({10^{ - 3}})(1) = {10^{ - 3}}s = 1\,ms$$
$$i = {i_0}(1 - {e^{ - t/{\tau _L}}}) = {{{{10}^{ - 3}}} \over 1}(1 - {e^{ - 1}})$$
$$i = {10^{ - 3}}(1 - 0.37)$$
i = 0.63 mA
$$e = (v \times B)dl = {10^{ - 2}} \times 1 \times {10^{ - 1}}$$
e = $${10^{ - 3}}V$$
$${\tau _L} = LR = ({10^{ - 3}})(1) = {10^{ - 3}}s = 1\,ms$$
$$i = {i_0}(1 - {e^{ - t/{\tau _L}}}) = {{{{10}^{ - 3}}} \over 1}(1 - {e^{ - 1}})$$
$$i = {10^{ - 3}}(1 - 0.37)$$
i = 0.63 mA
Comments (0)


