JEE Advance - Physics (2019 - Paper 2 Offline - No. 10)
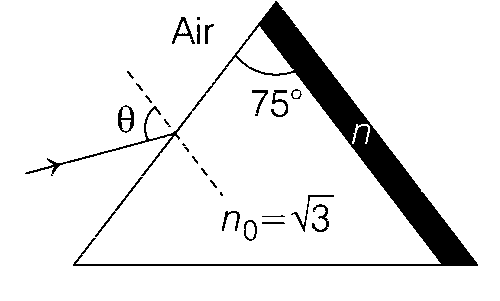
A monochromatic light is incident from air on a refracting surface of a prism of angle 75$$^\circ $$ and refractive index $${n_0} = \sqrt 3 $$. The other refracting surface of the prism is coated by a thin film of material of refractive index n as shown in figure. The light suffers total internal reflection at the coated prism surface for an incidence angle of $$\theta \le 60^\circ $$. The value of n2 is .............

Answer
1.50
Explanation
For TIR at coating,
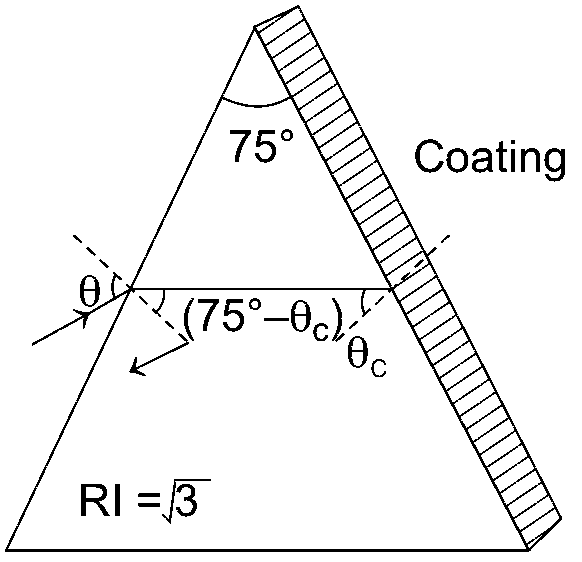
Applying Snell's law at first surface $$\sin \theta = \sqrt 3 \sin (75^\circ - {\theta _c})$$
For limiting condition, at $$\theta $$ = 60$$^\circ $$
$$\sin 60^\circ = \sqrt 3 \sin (75^\circ - {\theta _c})$$
$${{\sqrt 3 } \over 2} = \sqrt 3 \sin (75^\circ - {\theta _c})$$
$${1 \over 2} = \sin (75^\circ - {\theta _c})$$
$$ \Rightarrow $$ $$sin30^\circ = \sin (75^\circ - {\theta _c})$$
$$30^\circ $$ = $$75^\circ - {\theta _c}$$ $$ \Rightarrow $$ $${\theta _c}$$ = 45$$^\circ $$
Now since θc < 60o, therefore total internal reflection takes place. For total internal reflection at the other refracting surface, using Snell’s law, we have
$${n \over {\sqrt 3 }} = {1 \over {\sqrt 2 }} \Rightarrow {n^2} = {3 \over 2} = 1.50$$

Applying Snell's law at first surface $$\sin \theta = \sqrt 3 \sin (75^\circ - {\theta _c})$$
For limiting condition, at $$\theta $$ = 60$$^\circ $$
$$\sin 60^\circ = \sqrt 3 \sin (75^\circ - {\theta _c})$$
$${{\sqrt 3 } \over 2} = \sqrt 3 \sin (75^\circ - {\theta _c})$$
$${1 \over 2} = \sin (75^\circ - {\theta _c})$$
$$ \Rightarrow $$ $$sin30^\circ = \sin (75^\circ - {\theta _c})$$
$$30^\circ $$ = $$75^\circ - {\theta _c}$$ $$ \Rightarrow $$ $${\theta _c}$$ = 45$$^\circ $$
Now since θc < 60o, therefore total internal reflection takes place. For total internal reflection at the other refracting surface, using Snell’s law, we have
$${n \over {\sqrt 3 }} = {1 \over {\sqrt 2 }} \Rightarrow {n^2} = {3 \over 2} = 1.50$$
Comments (0)


