JEE Advance - Physics (2019 - Paper 2 Offline - No. 3)
Three glass cylinders of equal height H = 30 cm and same refractive index n = 1.5 are placed on a horizontal surface as shown in figure.
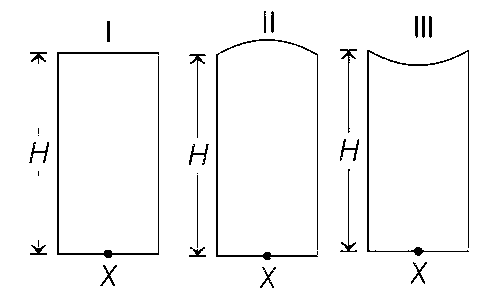
Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (R = 3 m). If H1, H2, and H3 are the apparent depths of a point X on the bottom of the three cylinders, respectively, the correct statement(s) is/are
Cylinder I has a flat top, cylinder II has a convex top and cylinder III has a concave top. The radii of curvature of the two curved tops are same (R = 3 m). If H1, H2, and H3 are the apparent depths of a point X on the bottom of the three cylinders, respectively, the correct statement(s) is/are
H2 > H1
H3 > H1
0.85 cm < (H2 $$ - $$ H1) < 0.9 cm
H2 > H3
Explanation
Case - I
H = 30 cm
n = $${3 \over 2}$$
H1 = $${H \over n}$$
$$ \Rightarrow $$ $${{30 \times 2} \over 3}$$ = 20 cm
Case - II
R = 300 cm
$${{{n_2}} \over v} - {{{n_1}} \over u} = {{{n_2} - {n_1}} \over R}$$
$${1 \over { - {H_2}}} - {3 \over { - 2 \times 30}} = {{1 - {3 \over 2}} \over { - 300}}$$
$${H_2} = {{600} \over {29}} = 20.684$$ cm
Case - III
$${{{n_2}} \over v} - {{{n_1}} \over u} = {{{n_2} - {n_1}} \over R}$$;
$${1 \over { - {H_3}}} - {3 \over { - 2 \times 30}} = {{1 - {3 \over 2}} \over {300}}$$
$${H_3} = {{600} \over {31}} = 19.354$$ cm
H = 30 cmn = $${3 \over 2}$$
H1 = $${H \over n}$$
$$ \Rightarrow $$ $${{30 \times 2} \over 3}$$ = 20 cm
Case - II
R = 300 cm$${{{n_2}} \over v} - {{{n_1}} \over u} = {{{n_2} - {n_1}} \over R}$$
$${1 \over { - {H_2}}} - {3 \over { - 2 \times 30}} = {{1 - {3 \over 2}} \over { - 300}}$$
$${H_2} = {{600} \over {29}} = 20.684$$ cm
Case - III
$${{{n_2}} \over v} - {{{n_1}} \over u} = {{{n_2} - {n_1}} \over R}$$;$${1 \over { - {H_3}}} - {3 \over { - 2 \times 30}} = {{1 - {3 \over 2}} \over {300}}$$
$${H_3} = {{600} \over {31}} = 19.354$$ cm
Comments (0)
