$$20 \mathrm{~cm}$$ व्यास वाले एक छोटे बेलन (roller) की धुरी (axle) का व्यास $$10 \mathrm{~cm}$$ है (नीचे दिखाए गए बाएं चित्र को देखें ) | यह एक क्षैतिज तल पर रखा हुआ है । एक क्षैतिज मीटर स्केल का एक छोर इसकी धुरी के ऊपर रखा हुआ है (नीचे दिखाए गए दाएं चित्र को देखें ) इस स्केल को अब धीरे-धीरे धुरी पर इस प्रकार धकेला जाता है कि स्केल धुरी पर बिना फिसले चलता है, एवं बेलन बिना फिसले लोटन करना आरम्भ करता है। बेलन के $$50 \mathrm{~cm}$$ आगे बढ़ चुकने के पश्चात, स्केल की स्थिति निम्न में से किस तरह दिखाई देगी (चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है )

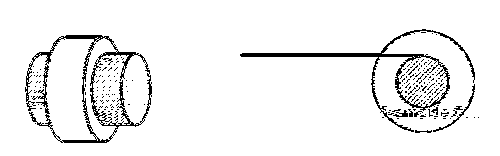
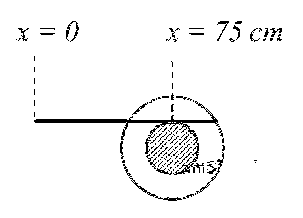
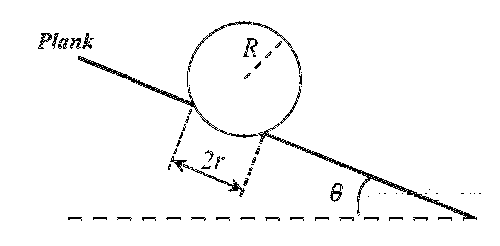
क्षैतिज अवस्था में रखे हुए एक तखे (plank) में एक छिद्र है जिसकी त्रिज्या $r$ है। तख्ते के इस छिद्र पर एक $$R(R > r)$$ त्रिज्या वाले फुटबॉल को रखा गया है । जैसा कि नीचे चित्र में दिखाया गया है, इस तख्ते को अब एक छोर से ऊपर उठाया जाता है जिससे कि यह उत्रत हो कर क्षितिज से $$\theta$$ का कोण बनाता है। $$\theta$$ का अधिकतम मान जब तक कि फुटबॉल तख्ते पर लोटना प्रारंभ नहीं करती है, इस तरह है कि हचित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है ]

एक स्थिर स्वरित्र द्विभुज (tunning fork), एक नलिका (pipe) के वायु कॉलम के साथ अनुनाद (resonance) की अवस्था में है । अब यह स्वरित्र द्विभुज, नलिका के खुले छोर के सामने एवं इसकी समांतर दिशा में $$2 \mathrm{~ms}^{-1}$$ गति से चलाया जाता है। इस स्थिति में गतिमान स्वरित्र द्विभुज के साथ अनुनादी होने के लिए नलिका की लम्बाई में परिवर्तन करना पड़ेगा । यदि वायु में ध्वनि की चाल $$320 \mathrm{~m} \mathrm{~s}^{-1}$$ है, तब नलिका की लम्बाई में होने वाला प्रतिशत परिवर्तन का न्यूनतम मान _____________ है ।

एक वृत्ताकार चक्रिका (disc), जिसकी त्रिज्या $$R$$ है, पर पृष्ठीय आवेश घनत्व $$\sigma(r)=\sigma_{o}\left(1-\frac{r}{R}\right)$$ है, जहां $$\sigma_{o}$$ एक स्थिरांक है एवं $r$ चक्रिका के केंद्र से दूरी है । एक बड़े गोलीय पृष्ठ, जो इस आवेशित चक्रिका को पूरी तरह से परिबद्ध (enclose) करता है, से गुजरने वाला वैद्युत फ्लक्स $$\phi_{o}$$ है। एक अन्य गोलीय पृष्ठ, जो चक्रिका के साथ संकेंद्रित है एवं जिसकी त्रिज्या $$\frac{R}{4}$$ है, से गुजरने वाला वैद्युत फ्लक्स $$\phi$$ है । तब अनुपात $$\frac{\phi_{o}}{\phi}$$ का मान ____________ है।

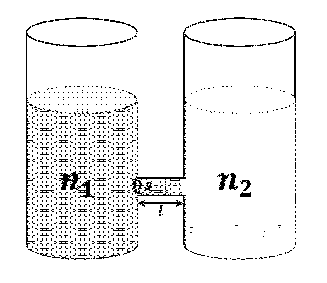
प्रतीकात्मक चित्रानुसार, दो पात्रों में पोटेशियम परमैंगनेट $$\left(\mathrm{KMnO}_{4}\right)$$ के जलीय विलियन तापमान $$T$$ पर रखे हुये हैं। पात्रों में इन घोलों की सांद्रताएँ क्रमशः $$n_{1}$$ तथा $$n_{2}\left(n_{1} > n_{2}\right)$$ अणु प्रति एकक आयतन हैं, जहां $$\Delta n=\left(n_{1}-n_{2}\right) \ll n_{1}$$ है | दोनों पात्रों को एक छोटी नलिका के द्वारा जोड़े जाने पर $$\mathrm{KMnO}_{4}$$ बाएं पात्र से दाएं पात्र में इस नलिका के द्वारा विसरण (diffusion) करना आरम्भ करता है। छोटी नलिका की लम्बाई $$l$$ तथा अनुप्रस्थ काट का क्षेत्रफल $$S$$ है। परिकल्पना करिए कि अणुओं का यह समूह तनु आदर्श गैस के अनुरूप आचरण करता है, तथा अणुओं का विसरण दोनों पत्रों में उनके आंशिक दाब के अंतर के कारण होता है। इन अणुओं की चाल $$v$$ प्रत्येक अणु पर लगे श्यानता बल (viscous force) $$-\beta v$$ के द्वारा सीमित होती है, जहां $$\beta$$ एक नियतांक है। $$(\Delta n)^{2}$$ वाले सभी पदों को नगण्य मानते हुए, निम्न में से कौन सा (से) कथन सही है (हैं)? ($$k_{B}$$ बोल्ज्ञान नियतांक है)

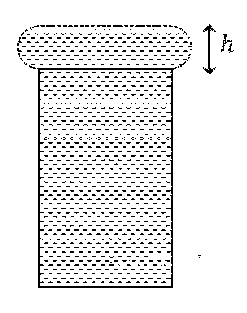
यदि एक गिलास में सावधानी पूर्वक जल भरा जाय तो जल के पृष्ठ तनाव के कारण इसे गिलास के किनारों से ऊपर $$h$$ ऊँचाई तक भरा जा सकता है | इस ऊँचाई की गणना करने के लिए हम परिकल्पना करते हैं कि गिलास से जल के अधिप्रवाह (flow) से पूर्व, गिलास के किनारों से ऊपर का जल, प्रतीकात्मक चित्रानुसार, $$h$$ मोटाई की एक चक्रिका (disk) के आकार में है, जिसके किनारे अर्ध वृत्ताकार हैं। जब जल का दबाव इस चक्रिका के निचले भाग पर इतना हो जाता है कि पृष्ठ तनाव के कारण उत्पत्न बल इससे कम हो जाय तो गिलास के किनारों के निकट जल का पृष्ठ टूट जाता है तथा यहाँ से जल बहने लगता है । यदि जल का घनत्व, जल का पृष्ठ-तनाव तथा गुरुत्वीय त्वरण का मान क्रमशः $$10^{3} \mathrm{~kg} \mathrm{~m}^{-3}, 0.07 ~\mathrm{Nm}^{-1}$$ तथा $$10 \mathrm{~ms}^{-2}$$ हो, तो का $$h$$ मान $$\mathrm{mm}$$ में ____________ होगा ।

आप अपने हाथों की पूर्णतः खुली हुई तर्जनी उंगलियों पर एक मीटर लम्बे एकसमान पैमाने (scale) को क्षैतिज अवस्था में इस प्रकार रखें कि बाईं उंगली $$0.00 \mathrm{~cm}$$ पर तथा दायीं उंगली $$90.00 \mathrm{~cm}$$ पर हो । जब आप ऊंगलियों को पैमाने के केंन्द्र की ओर धीरे-धीरे चलाकर लाने का प्रयत्न करते हैं, तब आरम्भ में केवल बाईं ऊंगली ही पैमाने के सापेक्ष फिसलती है तथा दायीं ऊंगली नहीं चलती है। कुछ दूरी चलने के बाद बाईं ऊंगली रुक जाती है तथा अब दायीं ऊंगली फिसलना आरम्भ करती है। पैमाने के केंद्र $$(50.00 \mathrm{~cm})$$ से $$x_{R}$$ दूरी पर आ कर दायीं ऊंगली रुक जाती है तथा बाईं ऊंगली पुनः फिसलना आरम्भ करती है। ऐसा दोनों ऊंगलियों पर लगने वाले घर्षण बलों के अंतर के कारण होता है। यदि उँगलियों तथा पैमाने के बीच के स्थैतिक घर्षण गुणांक का मान $$0.40$$ तथा गतिज घर्षण गुणांक का मान $$0.32$$ हो तो, $$\mathrm{cm}$$ में $$x_{R}$$ का मान ____________ होगा।

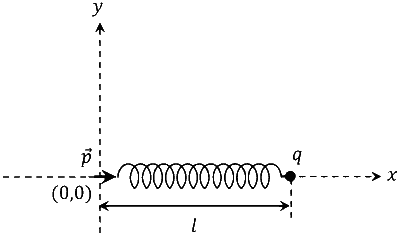
उपेक्षणीय अतानित (unstretched) लम्बाई की एक कमानी (spring), जिसका कमानी-नियतांक $$k$$ है, का एक सिरा मूल-बिंदु $$(0,0)$$ से सम्बद्ध (fixed) है। एक बिंदु-कण, जिसका द्रव्यमान $$m$$ तथा धनात्मक वैद्युत आवेश $$q$$ है, कमानी के दूसरे सिरे से सम्बद्ध है । यह निकाय एक चिकने क्षैतिज तल पर रखा गया है। यदि आवेश $$q$$ की ओर निर्दिष्ट, एक बिंदु-द्विध्रुव (point dipole) $$\vec{p}$$ को मूल-बिंदु पर सम्बद्ध किया जाय, तो खिंचाव के कारण निकाय की नई साम्यावस्था में कमानी की लम्बाई $$l$$ हो जाती है (नीचे चित्र देखें ) अब यदि बिंदुकण को साम्यावस्था से $$\Delta l(\Delta l \ll l)$$ विस्थापित करके मुक्त किया जाय तब यह $$\frac{1}{\delta} \sqrt{\frac{k}{m}}$$ की आवृत्ति से दोलन करता है | $$\delta$$ का मान _______________ है।

एक पात्र में परिबद्ध एक मोल हीलियम गैस का आरंभिक दाब $$P_{1}$$ एवं आयतन $$V_{1}$$ है । यह समतापीय (isothermal) प्रसरण करती है, जिससे की इसका आयतन $$4 V_{1}$$ हो जाता है । इसके पश्चात, गैस का रुद्धोष्म (adiabatic) प्रसरण होता है तथा इसका आयतन $$32 V_{1}$$ हो जाता है । समतापीय एवं रुद्धोष्म प्रसरण के समय गैस द्वारा किये गए कार्य क्रमशः $$W_{i s o}$$ तथा $$W_{\text {adia }}$$ हैं । यदि अनुपात $$\frac{W_{\text {iso }}}{W_{\text {adia }}}=f \ln 2$$ है, तो $$f$$ का मान __________ है ।

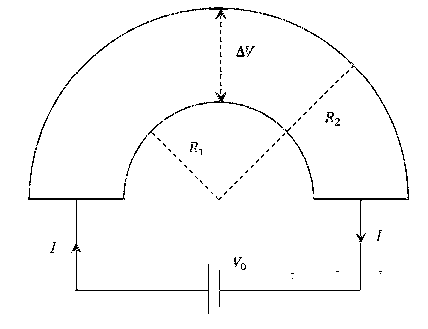
चित्र में दर्शायी गयी एक अर्धवृत्ताकार धात्विक पट्टी की मोटाई $t$, प्रतिरोधकता (resistivity) $$\rho$$, आतंरिक त्रिज्या $$R_{1}$$ एवं बाह्य त्रिज्या $$R_{2}$$ है | इस पट्टी के दोनों सिरों के मध्य विभवान्तर $$V_{0}$$ होने पर इसमें प्रवाहित विद्युत् धारा $$I$$ है | इसके अतिरिक्त, यह देखा जाता है कि पट्टी के आतंरिक एवं बाह्य पृष्ठ के मध्य एक अनुप्रस्थ (transverse) विभवान्तर $$\Delta V$$ है, जो विशुद्ध रूप से गतिमान इलेक्ट्रानों के गतिज प्रभावों (kinetic effects) के कारण उत्पत्र होता है (विद्युत् धारा से उत्पन्न चुम्बकीय क्षेत्र की भूमिका नगण्य मानें ) । तद्नुसार [चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है]

द्रव्यमान $$m$$ के एक कण की स्थितिज ऊर्जा (potential energy) $$V(r)=F r$$ है तथा यह वृत्ताकार कक्षाओं में घूमता है | यहाँ $$F$$ एक धनात्मक नियतांक है, तथा कण की मूल-बिंदु से दूरी $$r$$ है। कण की ऊर्जाओं की गणना बोहर मॉडल (Bohr's Model) के द्वारा की जाती है। यदि कण की कक्षा की त्रिज्या $$R$$, तथा इसकी गति एवं ऊर्जा क्रमशः, $$v$$ एवं $$E$$ हैं, तब $$n$$ वीं कक्षा के लिए (यहाँ $$h$$ प्लांक नियतांक है)

कभी कभी मात्रकों की एक ऐसी प्रणाली को बनाना सुविधाजनक होता है, जिसमें सभी राशियों को केवल एक भौतिक राशि के रूप में व्यक्त किया जा सके। ऐसी ही एक प्रणाली में अलग अलग राशियों की विमाओं को एक राशि $$X$$ के रूप में इस प्रकार से व्यक्त करते हैं कि: [स्थिति ]$$=\left[X^{\alpha}\right]$$; [चाल]$$=\left[X^{\beta}\right]$$; [त्वरण] $$=\left[X^{p}\right]$$; [रेखीय संवेग ]$$=\left[X^{q}\right]$$ ; [बल ] $$=\left[X^{r}\right]$$ | तब

एक प्रकाशीय बल्ब के तंतु (filament) का पृष्ठीय क्षेत्रफल $$64 \mathrm{~mm}^{2}$$ है । इस तंतु को $$2500 \mathrm{~K}$$ तापमान वाली एक कृष्णिका (black body) के तरह मान सकते हैं जो कि दूर से देखने पर एक बिंदु स्रोत की भांति विकिरण उत्सर्जित करता है। इस प्रकाशीय बल्ब को रात्रि में $$100 \mathrm{~m}$$ की दूरी से देखा जाता है। मान लीजिये कि प्रेक्षक की आँखों की पुतली वृत्ताकार है एवं इसकी त्रिज्या $$3 \mathrm{~mm}$$ है । तब

(स्टीफन-बोल्त्ज्मान नियतांक $$=5.67 \times 10^{-8} \mathrm{Wm}^{-2} \mathrm{~K}^{-4}$$, वीन का विस्थापन नियतांक $$=2.90 \times10^{-3} \mathrm{~m}-\mathrm{K}$$, प्लांक नियतांक $$=6.63 \times 10^{-34} \mathrm{Js}$$, निर्वात में प्रकाश की गति $$\mathrm{c}=3.00 \times 10^{8} \mathrm{~ms}^{-1}$$ लीजिए)

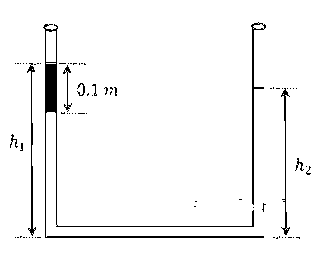
एकसमान अनुप्रस्थ काट के क्षेत्रफल वाली $$\mathrm{U}-$$ नली, जिसके दोनों सिरे खुले हुए हैं, में जल भरा है। जल का घनत्व $$10^{3} \mathrm{~kg} \mathrm{~m}^{-3}$$ है। आरम्भ में $$\mathrm{U}-$$ नली की दोनों भुजाओं में जल स्तम्भ की ऊंचाई, नली की पेंदी के सापेक्ष $$0.29 \mathrm{~m}$$ है |$$\mathrm{U}$$-नली की बाईं भुजा में किरोसिन तेल तब तक डाला जाता है जब तक इसकी ऊंचाई $$0.1 \mathrm{~m}$$ न हो जाये, जैसा की चित्र में दर्शाया गया है। किरोसिन तेल एक जल में अघुलनशील द्रव है तथा इसका घनत्व $$800 \mathrm{~kg} \mathrm{~m}^{-3}$$ है । नली की दोनों भुजाओं में द्रव स्तंभों की ऊंचाई का अनुपात $$\left(\frac{h_{1}}{h_{2}}\right) $$ ____________ है।

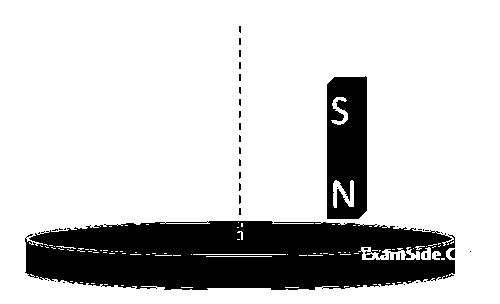
एलुमिनियम (एक अचुम्बकीय पदार्थ) से बनी एक हल्की चक्रिका (disc) क्षैतिज अवस्था में रखी है एवं यह अपने अक्ष (axis) के परितः घूर्णन करने के लिए स्वतंत्र है, जैसा कि नीचे चित्र में दिखाया गया है। यदि एक प्रबल चुम्बक को चक्रिका से थोड़ा ऊपर, उसके अक्ष से दूर एक बिंदु पर ऊर्ध्वाधर अवस्था में रखते हुए चक्रिका के अक्ष के परितः परिक्रमण (revolve) कराया जाय तब चक्रिका [चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है ]

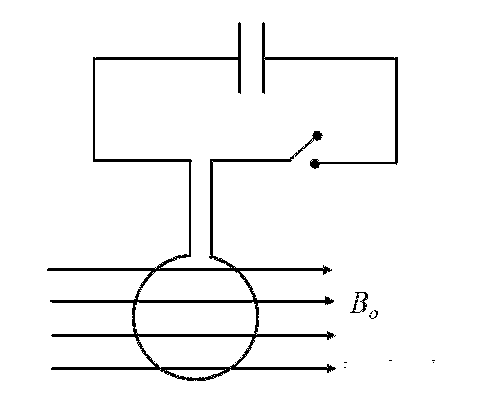
एक वृत्ताकार कुण्डली, जिसकी त्रिज्या $$R$$ एवं फेरों की संख्या $$N$$ है, का प्रतिरोध (resistance) नगण्य है । जैसा की चित्र में दर्शाया गया है, इसके दो छोर दो तारों से जुड़े हुए हैं, तथा यह उन तारों के द्वारा इस प्रकार लटकी हुई है कि इसका तल ऊर्ध्वाधर (vertical) है। दोनों तार एक संधारित्र (capacitor), जिस पर आवेश $$Q$$ है, से एक स्विच के द्वारा जुड़े हुए हैं। यह कुण्डली एक एकसमान क्षैतिज चुम्बकीय क्षेत्र, जो कि कुण्डली के तल के समांतर है तथा जिसकी तीव्रता $$B_{o}$$ है, में स्थित है। जब स्विच को बंद करते हैं तो संधारित्र कुण्डली के माध्यम से अति अल्प समय में ही अनावेशित हो जाता है। जितने समय में यह संधारित्र पूरी तरह से अनावेशित हो जाता है, उतने समय में कुण्डली द्वारा प्राप्त कोणीय संवेग (angular momentum) का मान निम्न में से कौन सा होगा (यह मानिए कि अनावेश समय इतना लघु है कि कुण्डली इस समय में नाममात्र ही घूम पाती है)

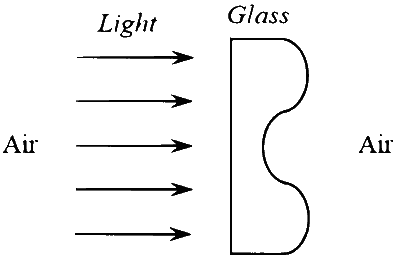
प्रकाश का एक समांतर किरण पुंज काँच के एक पारदर्शी टुकड़े, जिसकी अनुप्रस्थ काट नीचे दिए चित्रानुसार है, पर आपतित होता है | तब निर्गत तरंगाग्र (emergent wavefront) की सही आकृति इस प्रकार होगी [चित्र प्रतीकात्मक (schematic) हैं तथा माप के अनुसार नहीं है; Air: हवा; Light: प्रकाश; Glass: काँच]

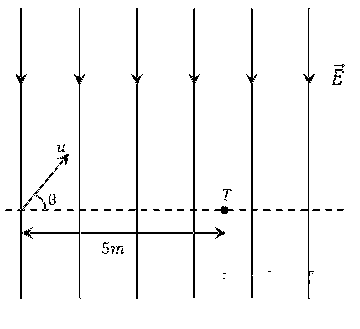
किसी क्षेत्र में एकसमान विद्युत क्षेत्र, $$\vec{E}=-400 \sqrt{3} \hat{y} \mathrm{~NC}^{-1}$$ लगाया गया है। द्रव्यमान $$m$$ के एक धनावेशित कण को, जिस पर आवेश $$q$$ है, इस क्षेत्र में $$2 \sqrt{10} \times 10^{6} \mathrm{~ms}^{-1}$$ की आरंभिक गति से प्रक्षेपित किया जाता है | इस कण को प्रक्षेपित करने का उद्द्येश्य, क्षेत्र में प्रवेश बिंदु से $$5 \mathrm{~m}$$ की क्षैतिज दूरी पर रखे लक्ष्य $$\mathrm{T}$$ को भेदना है, जैसा कि चित्र में प्रतीकात्मक (schematic) रूप से दर्शाया गया है । यदि $$\frac{q}{m}=10^{10} \mathrm{C} \mathrm{~kg}^{-1}$$, तो