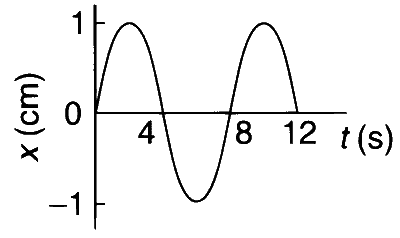
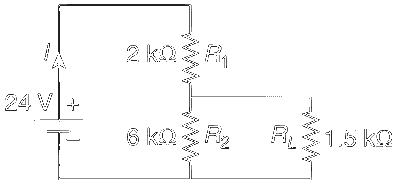
JEE Advance - Physics (2009 - Paper 1 Offline)
Look at the drawing given in the figure below which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is $$m$$. the mass of the ink used to draw the outer circle is $$6m$$. The coordinates of the centres of the different parts are: outer circle (0, 0), left inner circle ($$-a,a$$), right inner circle ($$a,a$$), vertical line (0, 0) and horizontal line ($$0,-a$$). The y-coordinate of the centre of mass of the ink in this drawing is
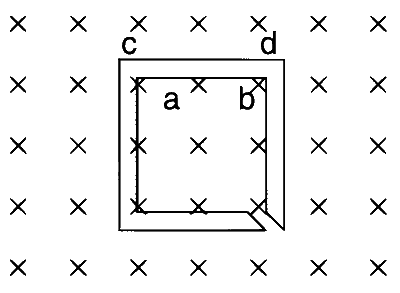
The figure shows certain wire segments joined together to form a coplanar loop. The loop is placed in a perpendicular magnetic field in the direction going into the plane of the figure. The magnitude of the field increases with time. $$I_1$$ and $$I_2$$ are the currents in the segments ab and cd. Then,
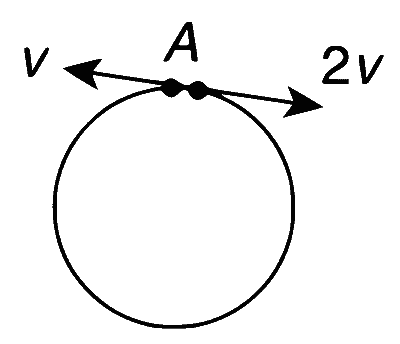
Two small particles of equal masses start moving in opposite directions from a point A in a horizontal circular orbit. Their tangential velocities are $$v$$ and 2$$v$$, respectively, as shown in the figure. Between collisions, the particles move with constant speeds. After making how many elastic collisions, other than that at A, these two particles will again reach the point A?
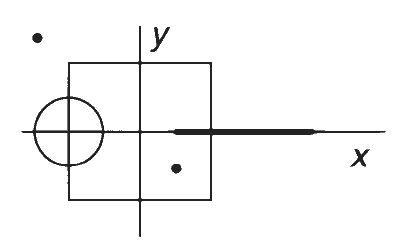
A disk of radius $${a \over 4}$$ having a uniformly distributed charge 6C is placed in the xy-plane with its centre at ($$-$$a/2, 0, 0). A rod of length a carrying a uniformly distributed charge 8C is placed on the x-axis from x = a/4 to x = 5a/4. Two points charges $$-$$7C and 3C are placed at (a/4, $$-$$a/4, 0) and ($$-$$3a/4, 3a/4, 0), respectively. Consider a cubical surface formed by six surfaces $$x=\pm a/2,y=\pm a/2,z=\pm a/2$$. The electric flux through this cubical surface is
Column II shows five systems in which two objects are labelled as X and Y. Also in each case a point P is shown. Column I gives some statements about X and/or Y. Match these statements to the appropriate system(s) from Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | The force exerted by X on Y has a magnitude $$Mg$$. | (P) | 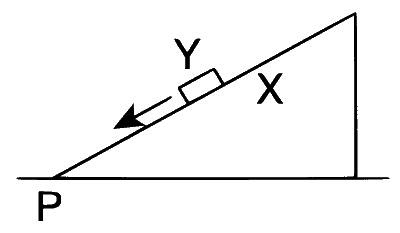 Block Y of mass M left on a fixed inclined plane X, slides on it with a constant velocity. |
| (B) | The gravitational potential energy of X is continuously increasing. | (Q) | 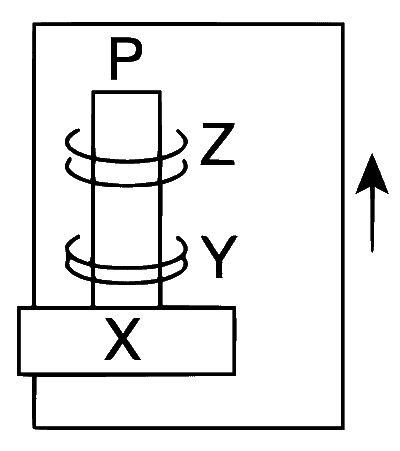 Two rings magnets Y and Z, each of mass M, are kept in frictionless vertical plastic stand so that they repel each other. Y rests on the base X and Z hangs in air in equilibrium. P is the topmost point of the stand on the common axis of the two rings. The whole system is in a lift that is going up with a constant velocity. |
| (C) | Mechanical energy of the system X + Y is continuously decreasing. | (R) | 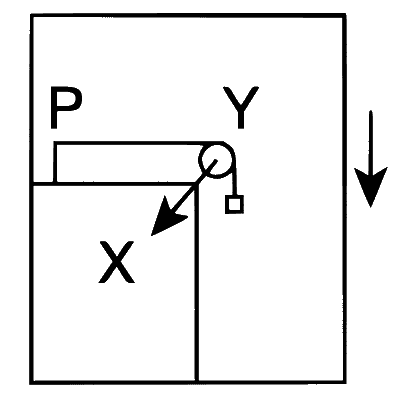 A pulley Y of mass $$m_0$$ is fixed to a table through a clamp X. A block of mass M hangs from a string that goes over the pulley and is fixed at point P of the table. The whole system is kept in a lift that is going down with a constant velocity. |
| (D) | The torque of the weight of Y about point is zero. | (S) | 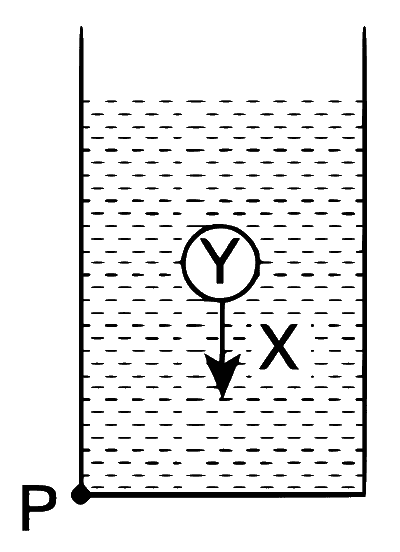 A sphere Y of mass M is put in a non-viscous liquid X kept in a container at rest. The sphere is released and it moves down in the liquid. |
| (T) | 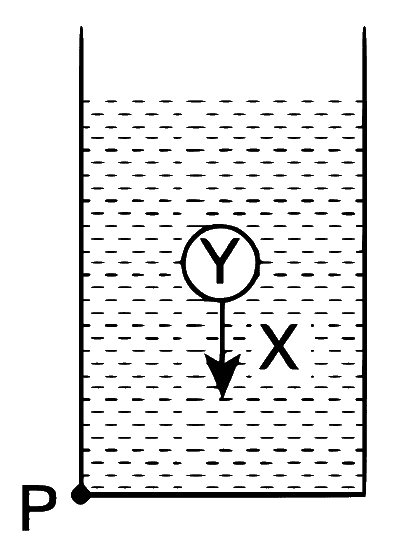 A sphere Y of mass M is falling with its terminal velocity in a viscous liquid X kept in a container. |
Six point charges, each of the same magnitude q, are arranged in different manners as shown in Column II. In each case, a point M and a line PQ passing through M are shown. Let E be the electric field and V be the electric potential at M (potential at infinity is zero) due to the given charge distribution when it is at rest. Now, the whole system is set into rotation with a constant angular velocity about the line PQ. Let B be the magnetic field at M and $$\mu$$ be the magnetic moment of the system in this condition. Assume each rotating charge to be equivalent to a steady current.
| Column I | Column II | ||
|---|---|---|---|
| (A) | $$E=0$$ | (P) | 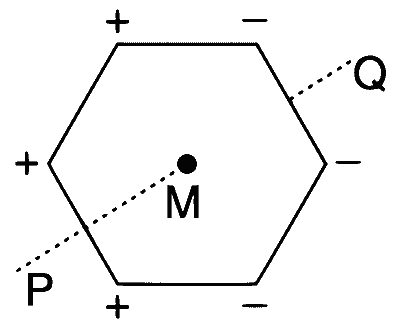 Charge are at the corners of a regular hexagon. M is at the centre of the hexagon. PQ is perpendicular to the plane of the hexagon. |
| (B) | $$V\ne 0$$ | (Q) | 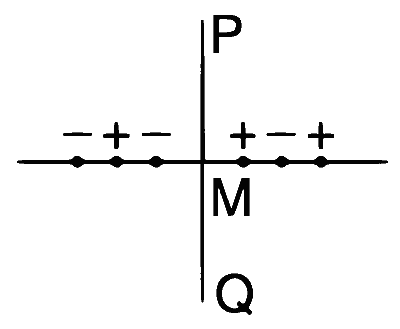 Charges are on a line perpendicular to PQ at equal intervals. M is the midpoint between the two innermost charges. |
| (C) | $$B=0$$ | (R) | 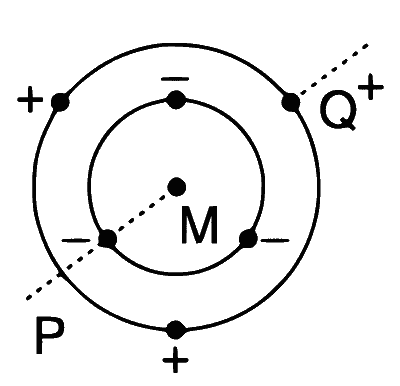 Charges are placed on two coplanar insulating rings at equal intervals. M is the common centre of the rings. PQ is perpendicular to the plane of the rings. |
| (D) | $$\mu \ne 0$$ | (S) | 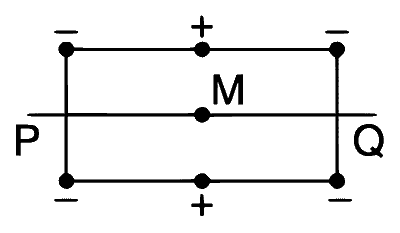 Charges are placed at the corners of a rectangle of sides a and 2a and at the mid points of the longer sides. M is at the centre of the rectangle. PQ is parallel to the longer sides. |
| (T) | 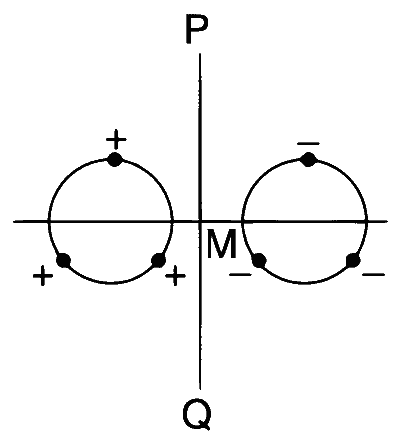 Charges are placed on two coplanar, identical insulating rings are equal intervals. M is the midpoint between the centres of the rings. PQ is perpendicular to the line joining the centres and coplanar to the rings. |