Sign In

JEE Advance - Physics (2009 - Paper 1 Offline - No. 20)

Six point charges, each of the same magnitude q, are arranged in different manners as shown in Column II. In each case, a point M and a line PQ passing through M are shown. Let E be the electric field and V be the electric potential at M (potential at infinity is zero) due to the given charge distribution when it is at rest. Now, the whole system is set into rotation with a constant angular velocity about the line PQ. Let B be the magnetic field at M and $$\mu$$ be the magnetic moment of the system in this condition. Assume each rotating charge to be equivalent to a steady current.

Column I Column II
(A) $$E=0$$ (P) 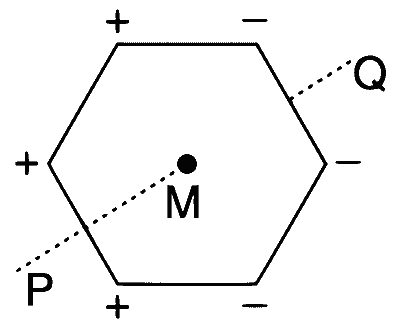IIT-JEE 2009 Paper 1 Offline Physics - Electrostatics Question 16 English 1
Charge are at the corners of a regular hexagon. M is at the centre of the hexagon. PQ is perpendicular to the plane of the hexagon.
(B) $$V\ne 0$$ (Q) 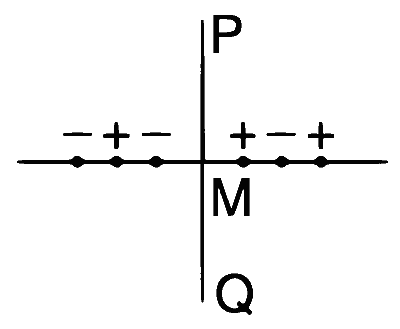IIT-JEE 2009 Paper 1 Offline Physics - Electrostatics Question 16 English 2
Charges are on a line perpendicular to PQ at equal intervals. M is the midpoint between the two innermost charges.
(C) $$B=0$$ (R) 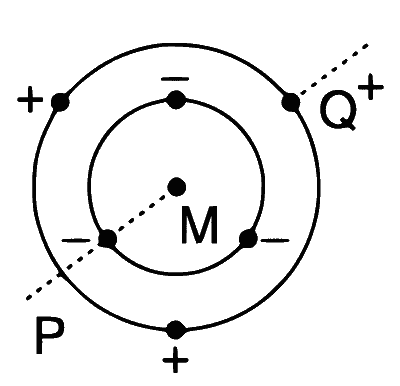IIT-JEE 2009 Paper 1 Offline Physics - Electrostatics Question 16 English 3
Charges are placed on two coplanar insulating rings at equal intervals. M is the common centre of the rings. PQ is perpendicular to the plane of the rings.
(D) $$\mu \ne 0$$ (S) 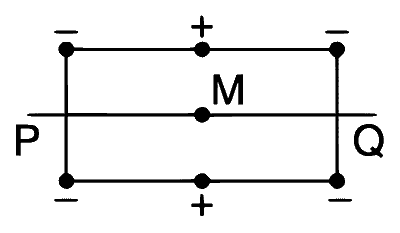IIT-JEE 2009 Paper 1 Offline Physics - Electrostatics Question 16 English 4
Charges are placed at the corners of a rectangle of sides a and 2a and at the mid points of the longer sides. M is at the centre of the rectangle. PQ is parallel to the longer sides.
(T) 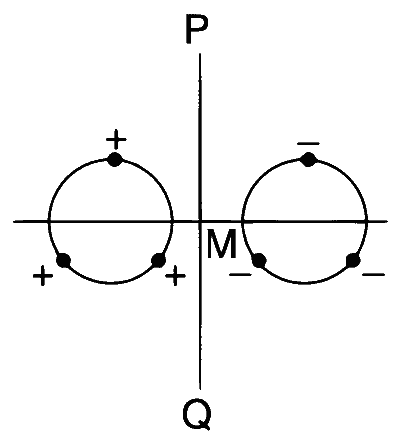IIT-JEE 2009 Paper 1 Offline Physics - Electrostatics Question 16 English 5
Charges are placed on two coplanar, identical insulating rings are equal intervals. M is the midpoint between the centres of the rings. PQ is perpendicular to the line joining the centres and coplanar to the rings.

$$\mathrm{(A)\to(R),(S);(B)\to(R),(S);(C)\to(P),(Q),(T);(D)\to(T),(S)}$$
$$\mathrm{(A)\to(P),(R),(S);(B)\to(R),(S);(C)\to(P),(Q),(S);(D)\to(R),(S)}$$
$$\mathrm{(A)\to(P),(R),(S);(B)\to(R),(S);(C)\to(P),(Q),(T);(D)\to(R),(S)}$$
$$\mathrm{(A)\to(P),(Q),(S);(B)\to(R),(S);(C)\to(P),(Q),(T);(D)\to(R),(S)}$$

Explanation

Case (P) : $$E=0,V=0, B=0,\mu=0$$.

Case (Q) : $$E\ne0,V=0, B=0,\mu=0$$.

Case (R) : $$E=0,V\ne0, B\ne0,\mu\ne0$$.

Case (S) : $$E=0,V\ne0, B\ne0,\mu\ne0$$.

Case (T) : $$E\ne0,V=0, B=0,\mu=0$$.

Hence, $$\mathrm{(A)\to(P),(R),(S);(B)\to(R),(S);(C)\to(P),(Q),(T);(D)\to(R),(S)}$$

Comments (0)

Advertisement