JEE Advance - Physics (2009 - Paper 1 Offline - No. 5)
A disk of radius $${a \over 4}$$ having a uniformly distributed charge 6C is placed in the xy-plane with its centre at ($$-$$a/2, 0, 0). A rod of length a carrying a uniformly distributed charge 8C is placed on the x-axis from x = a/4 to x = 5a/4. Two points charges $$-$$7C and 3C are placed at (a/4, $$-$$a/4, 0) and ($$-$$3a/4, 3a/4, 0), respectively. Consider a cubical surface formed by six surfaces $$x=\pm a/2,y=\pm a/2,z=\pm a/2$$. The electric flux through this cubical surface is
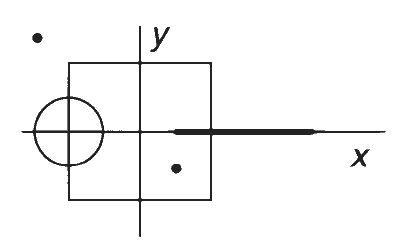
Explanation
According to Gauss's law, we have
$$\mathrm{Flux=\frac{Charge~enclosed}{\varepsilon_0}}$$
The enclosed charges are half of the charges in the disc, point charge at $$(a/4,-a/4,0)$$, and charge in the rod from point $$a/4$$ to $$a/2$$, that is, 8 C/4. Therefore,
Flux $$ = {{3C - 7C + (8C/4)} \over {{\varepsilon _0}}} = - {{2C} \over {{\varepsilon _0}}}$$
Comments (0)


