JEE Advance - Physics (2009 - Paper 1 Offline - No. 1)
A block of base 10 cm × 10 cm and height 15 cm is kept on an inclined plane. The coefficient of friction
between them is $$\sqrt 3 $$. The inclination θ of this inclined plane from the horizontal plane is gradually
increased from $$0^\circ $$. Then
at θ = $$60^\circ $$, the block will start sliding down the plane
the block will remain at rest on the plane up to certain θ and then it will topple
at θ = $$60^\circ $$, the block will start sliding down the plane and continue to do so at higher angles
at θ = $$60^\circ $$, the block will start sliding down the plane and on further increasing θ, it will topple at certain θ
Explanation
The block slides on the incline when
$$mg\sin \theta \ge \mu mg\cos \theta $$
$$ \Rightarrow \tan \theta \ge \mu $$
$$ \Rightarrow \tan \theta \ge \sqrt 3 = 1.732$$
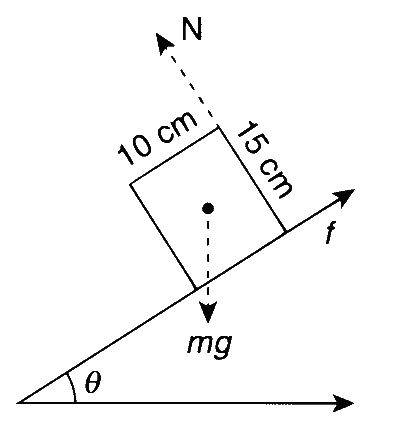
For the block to topple, we have
$$f\left( {{{15} \over 2}} \right) \ge N(5)$$ (about centre of mass)
$$ \Rightarrow \mu N\left( {{{15} \over 2}} \right) \ge N(5)$$
$$ \Rightarrow \mu \ge {2 \over 3} = 0.67$$
or $$\tan \theta \ge 0.67$$
That is, the block neither slides nor topples till $$\theta \le {\tan ^{ - 1}}(0.67)$$ (i.e. it remains at rest) and on exceeding this, it topples first before sliding.
Comments (0)


